0 引 言
在星载SAR 中,距离模糊指来自距离向方向图旁瓣的回波信号经过整数倍脉冲发射重复周期后,与目标点的回波信号一同被SAR 接收,从而对SAR 图像造成干扰的现象[1-2]。严重的距离模糊会使SAR图像中出现虚影[3],影响成像质量和图像解译,最终影响应用,因此合理的距离模糊比是星载SAR 系统设计的一项关键内容[4-5]。随着星载SAR的不断发展,大斜视成像成为目前SAR 发展的热门方向[6],而模糊信号的强弱与SAR系统的脉冲重复频率以及距离向波束宽度密切相关[7-8],大斜视成像下,斜距相对于正侧视下会增大,模糊区进入波束主瓣的可能性增大,使得距离模糊的性能变差,影响图像质量。因此对大斜视成像下的距离模糊进行研究有重要意义[9]。但目前公开文献中针对星载SAR 大斜视成像下距离模糊的研究较少。
距离模糊比很难通过实际测量得到,一般利用天线方向图和星地几何关系仿真计算得到[10-11]。目前距离模糊的仿真方法,都是以地球为球体模型作为假设条件[12],通过计算地心张角确定模糊区所在的位置[13],从而完成距离模糊比的计算。
大斜视成像下星地几何关系更为复杂,利用球体模型计算得到的距离模糊比会存在较大偏差。采用更为精确的地球椭球模型可以使计算结果更接近真实情况,但椭球模式下几何关系的计算比较复杂,本文提出了一种基于斜视天线坐标系的模糊区位置计算方法,用于简化计算。并利用该方法将椭球模型和球体模型下的距离模糊比沿距离向测绘带的变化进行仿真对比。由于星载SAR 大斜视成像下合成孔径时间长,斜距变化大,使得回波信号方位向与距离向的耦合变强,距离模糊比沿方位向空变性增强,本文也对模糊的空变性进行了仿真研究。
1 理论基础
1.1 距离模糊的定义
在SAR 成像过程中,如果天线波束旁瓣回波和主瓣回波的返回时间恰好相差整数倍的脉冲发射重复周期,此时接收到的回波信号将会是天线波束主瓣回波与旁瓣回波的混叠信号。在上述的混叠信号中,主瓣的回波信号为目标点信号,来自旁瓣的回波信号为模糊信号,模糊回波产生的位置定义为模糊点。目标点与模糊点的几何关系如图1所示。
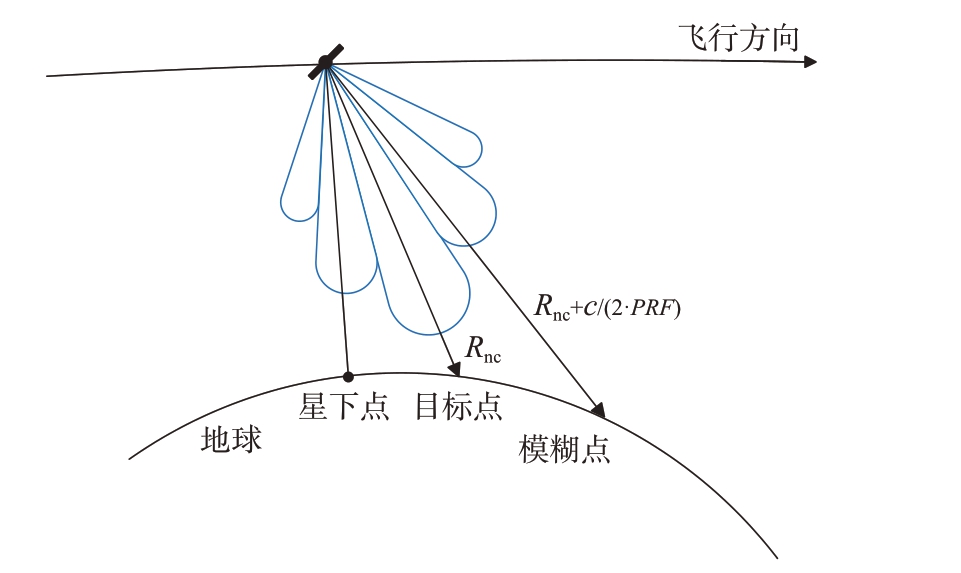
图1 距离模糊几何示意图
图中,目标点与卫星之间的距离为Rnc,c 为光速,PRF(Pulse Repetition Frequency)为脉冲发射重复频率,与卫星相距![]() 处的模糊点回波信号将在N个脉冲发射重复周期后被卫星接收。
处的模糊点回波信号将在N个脉冲发射重复周期后被卫星接收。
为了描述模糊信号的强弱,将模糊信号和有用信号的能量之比定义为距离模糊比。距离模糊比计算公式为[3]

式中:
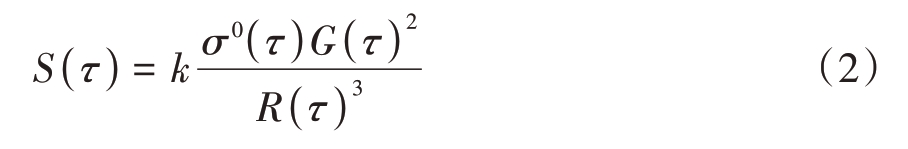
式中,n 为整数,代表第n 模糊区,τ 为方位向时间,σ0(τ)为地面后向散射系数,G(τ)为天线的方向图系数,R(τ)为天线相位中心与地面目标之间的距离,k为与方位向时间τ无关的其他项。
1.2 天线斜视坐标系定义
在传统模糊仿真中,通常利用简单的几何关系来计算斜距以及与波束中心的夹角,但该方法在斜视的情况下计算较为复杂,本文通过构造斜视天线坐标系,利用向量关系进行计算。
本文通过轨道六根数确定卫星位置,通过卫星姿态和天线位置确定天线相位中心,通过坐标转换的方式,将地心坐标系下的目标点坐标转换到以卫星天线相位中心为原点的天线坐标系下。各坐标系之间的转换关系示意图如图2所示[14]。

图2 各坐标系转换关系几何示意图
图中坐标系依次为地心转动坐标系Eg,地心不转动坐标系Eo,卫星轨道坐标系Ev,卫星平台坐标系Er,卫星星体坐标系Ee,天线坐标系Ea。
各坐标转换关系如下:
设天线相位中心相对于卫星星体坐标系的位置为![]() ,卫星相对于不转动地心坐标系的位置为
,卫星相对于不转动地心坐标系的位置为![]() 。假设目标点在天线坐标系中坐标为
。假设目标点在天线坐标系中坐标为![]() ,在地心转动坐标系的坐标为
,在地心转动坐标系的坐标为![]() ,则两者的转换关系为
,则两者的转换关系为
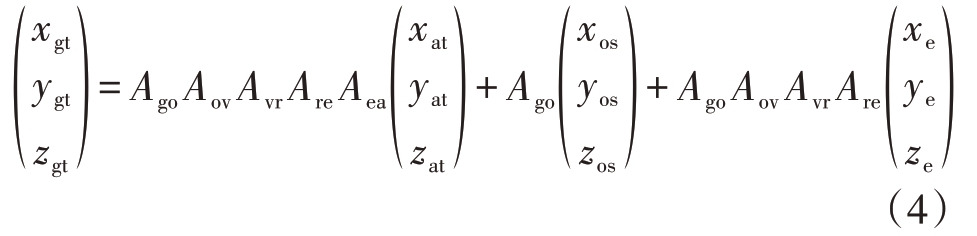
天线坐标系下,天线相位中心与原点o 重合,卫星飞行方向与x轴方向重合,正侧视时的天线波束指向方向与y 轴重合,因此在天线坐标系下xoy平面即为斜距平面,z 轴为该平面过天线相位中心的法线。
因此对场景内任意一点( )x, y, z 与天线波束相位中心之间的方位向夹角θps 和距离向夹角θds 可表示为
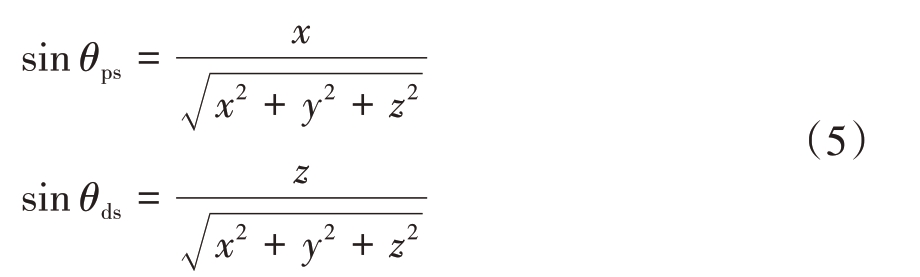
通过上述两个夹角,便可以计算得到点(x, y,z)位于方向图中的位置。
但在斜视情况下,天线波束指向与y轴并不在同一条直线上,使得上述公式不再适用,此时利用向量对方位向夹角和距离向夹角进行计算会变得复杂。为此将天线坐标系绕z 轴逆时针旋转斜视角θsq,引入一个新的天线斜视坐标系,转换矩阵A可表示为
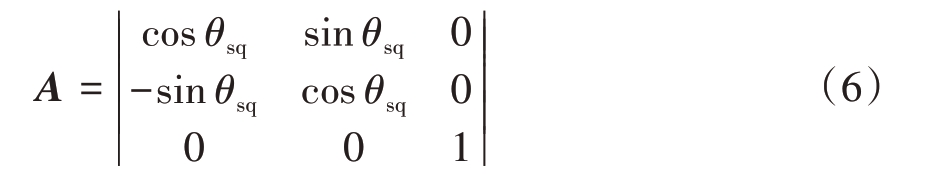
其几何示意图如图3所示。
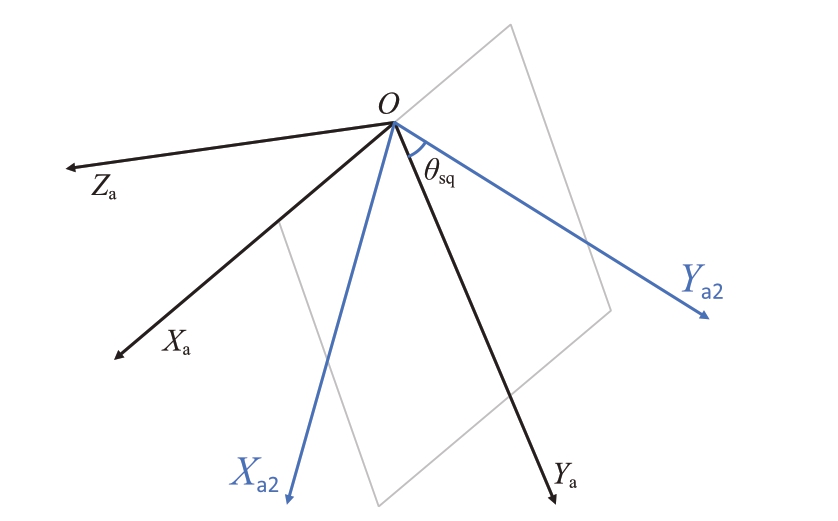
图3 天线斜视坐标系几何旋转示意图
天线斜视坐标系在经过旋转以后,其y轴仍然与波束指向重合,xoy 平面仍然为斜距平面,此时公式(5)依然适用。目标点的坐标转换关系变为
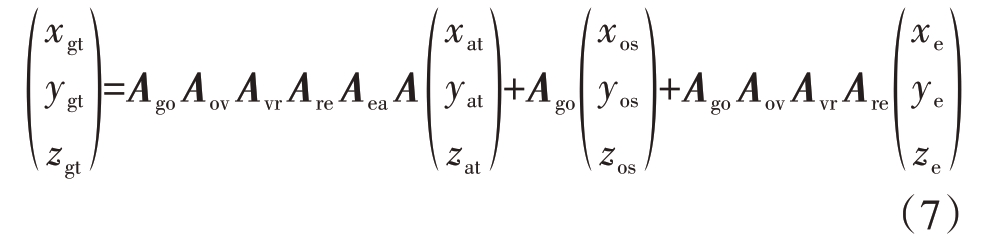
1.3 模糊区的计算
在传统的距离模糊计算中,通常假设地球为球体模型,即假设星下点、目标点以及模糊点所在位置的地球半径相同,这个假设在正侧视下带来的偏差可以忽略不计,但是在大斜视下,星地几何关系更加复杂,使得这个偏差较大,不能忽略,且目前利用地心距和角距计算模糊点位置的方法在椭球模型中并不适用,本文通过将RD 定位算法进行改进,将多普勒方程改为几何的斜视角方程,利用改进的RD 定位算法在斜视天线坐标系下的改进计算模糊区的位置。
定义天线坐标系中地心的坐标为(x0, y0, z0),目标点的坐标为(x1, y1, z1),模糊点所求坐标为(x, y, z)。三者的几何关系如图4所示。
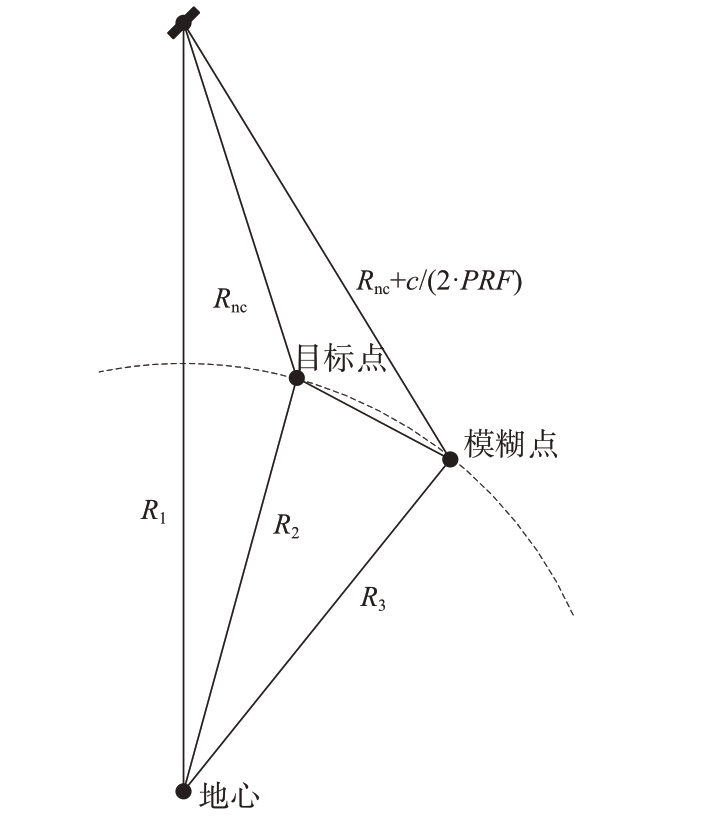
图4 距离模糊几何示意图
根据模糊的定义,模糊点与目标点具有相同的斜视角,但斜距不同,因此仅在下视角上存在不同,再根据图中的几何关系可以得到如下方程:
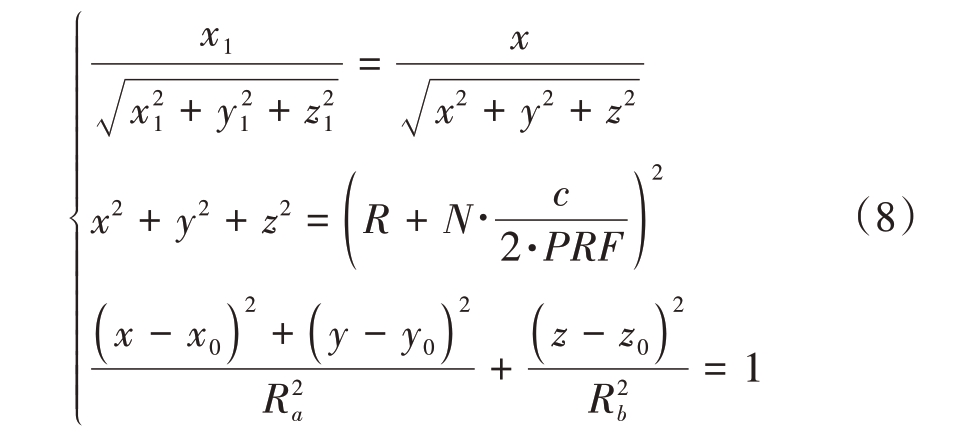
式中,R 为卫星与目标点之间斜距,c 为光速,PRF为SAR 采样频率,Ra 为地球椭圆模型长半轴,Rb 为地球椭圆模型短半轴。通过3 个方程可以求解得到模糊点的坐标( )x, y, z 。求解过程中,可先对变量x进行单独求解,再求解其他变量。
对变量x求解之后,方程可以被简化为
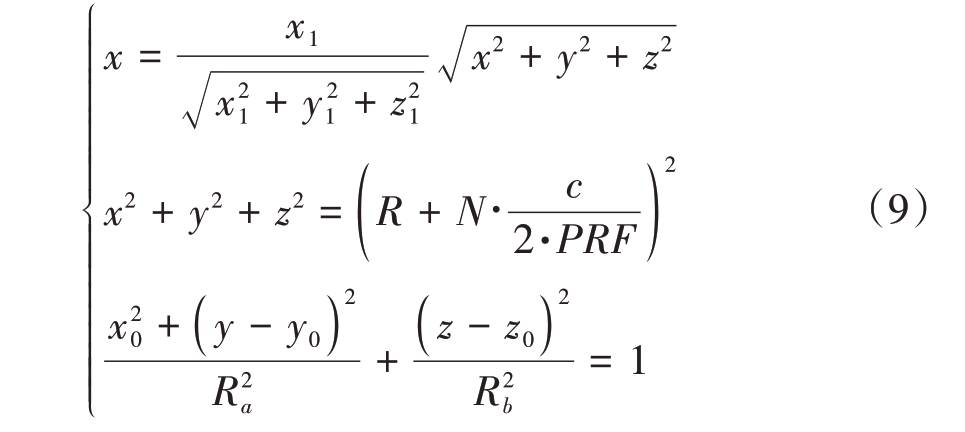
对方程进行进一步简化可得到
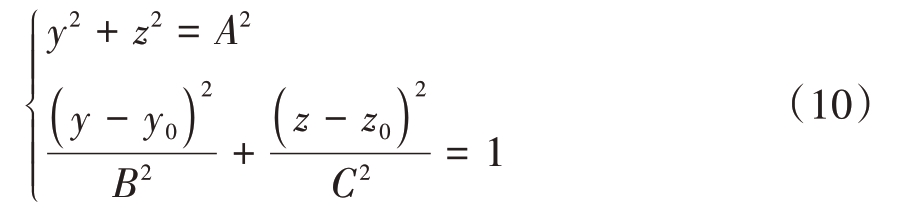
式中各参数如下:
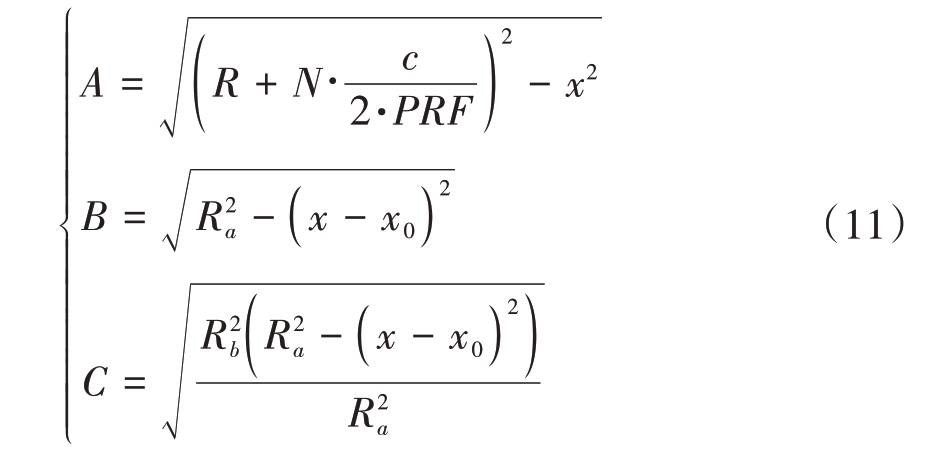
此时方程变为yoz 平面上圆与椭圆交点的几何问题,可以通过联立方程解一元四次方程对该问题进行求解。但一元四次方程求根公式复杂,为了更简便地求解此方程,将坐标系转化为极坐标系,即
代入方程后可得到
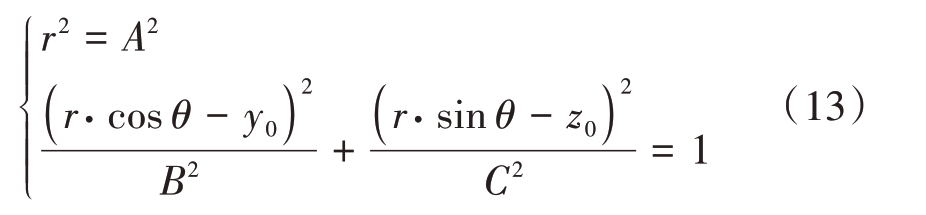
化简可以得到
此时方程便成为了只含有θ一个变量的函数,可以通过单变量的迭代求解。
2 仿真验证
仿真结果分为两部分:第一部分为距离模糊比沿距离向测绘带变化在椭球模型与球体模型下的对比仿真;第二部分为距离模糊比沿方位向的空变性仿真。
仿真过程中,假定后向散射系数为定值;距离向和方位向方向图形状均选用sinc函数,公式如下所示:
式中θ为方向图角度,βbw为天线波束宽度。
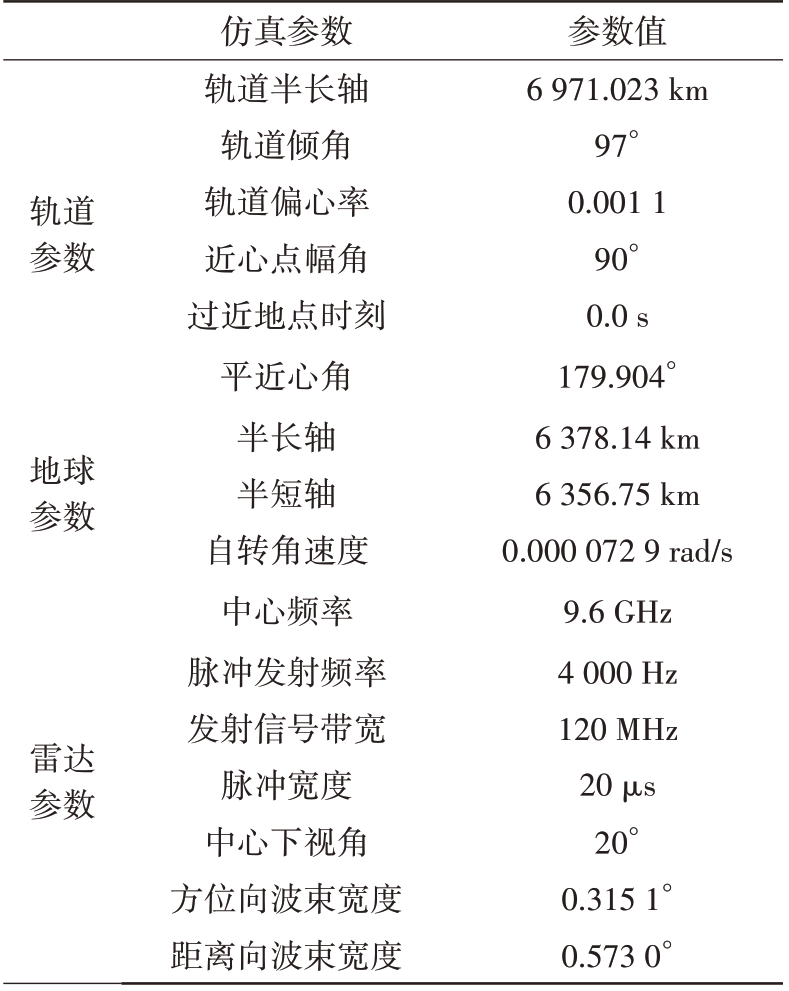
仿真中的主要参数如表1所示。
表1 仿真参数
轨道参数地球参数雷达参数仿真参数轨道半长轴轨道倾角轨道偏心率近心点幅角过近地点时刻平近心角半长轴半短轴自转角速度中心频率脉冲发射频率发射信号带宽脉冲宽度中心下视角方位向波束宽度距离向波束宽度参数值6 971.023 km 97°0.001 1 90°0.0 s 179.904°6 378.14 km 6 356.75 km 0.000 072 9 rad/s 9.6 GHz 4 000 Hz 120 MHz 20 μs 20°0.315 1°0.573 0°
2.1 距离模糊比沿距离向测绘带仿真
根据距离模糊比的原理,模糊区的位置与斜视角和PRF相关,因此本文分别对PRF为4 000 Hz与5 000 Hz 下的多斜视角进行仿真对比。仿真过程中,以表1中的地球长半轴和短半轴构建地球椭球模型,以地球长半轴为半径构建球体模型。将成像中心时刻的瞄准点作为场景中心,沿距离向测绘带前后2 500 m,每隔50 m 在地球上进行布点,示意图如图5所示。
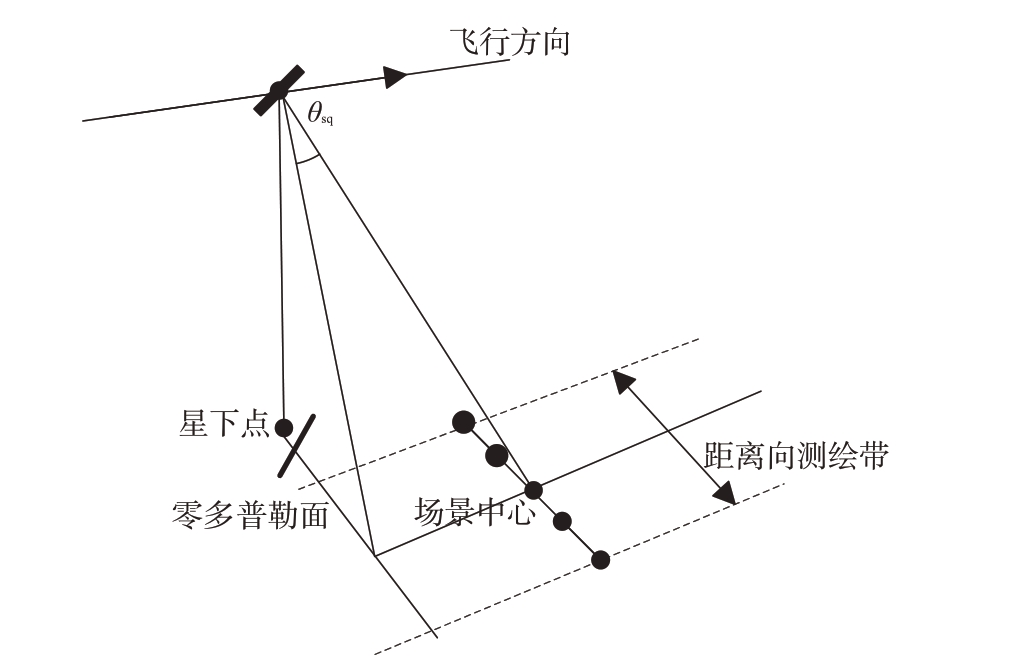
图5 点目标分布示意图
利用公式(5)、公式(7)计算得到目标点的斜距和位于方向图中的位置,利用公式(14)计算模糊区的位置,利用公式(1)计算距离模糊比,得到两种模型下的距离模糊比。PRF 为4 000 Hz 时的仿真结果如图6所示。
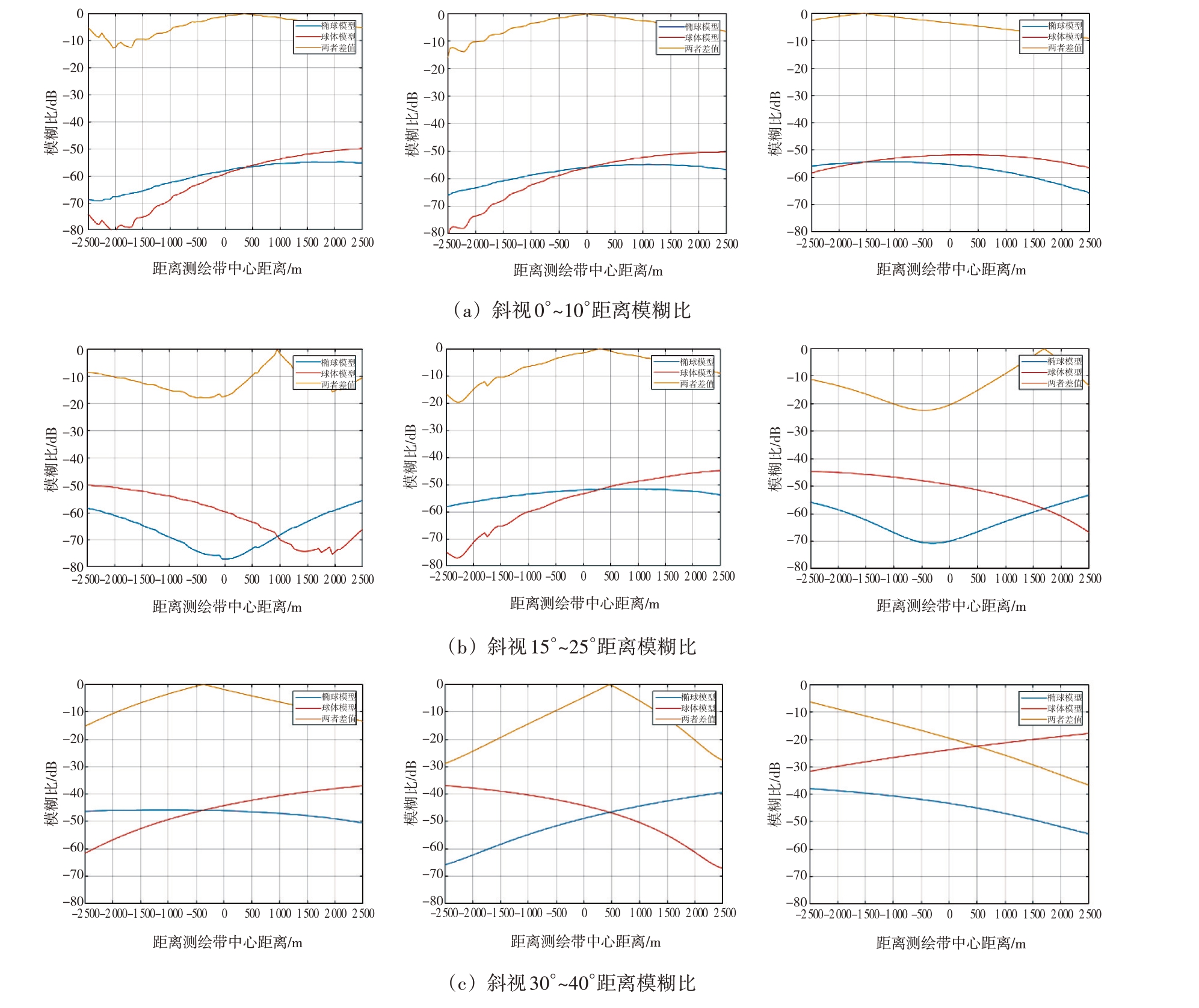
图6 PRF为4 000 Hz时距离模糊比曲线
PRF为5 000 Hz时的仿真结果如图7所示。
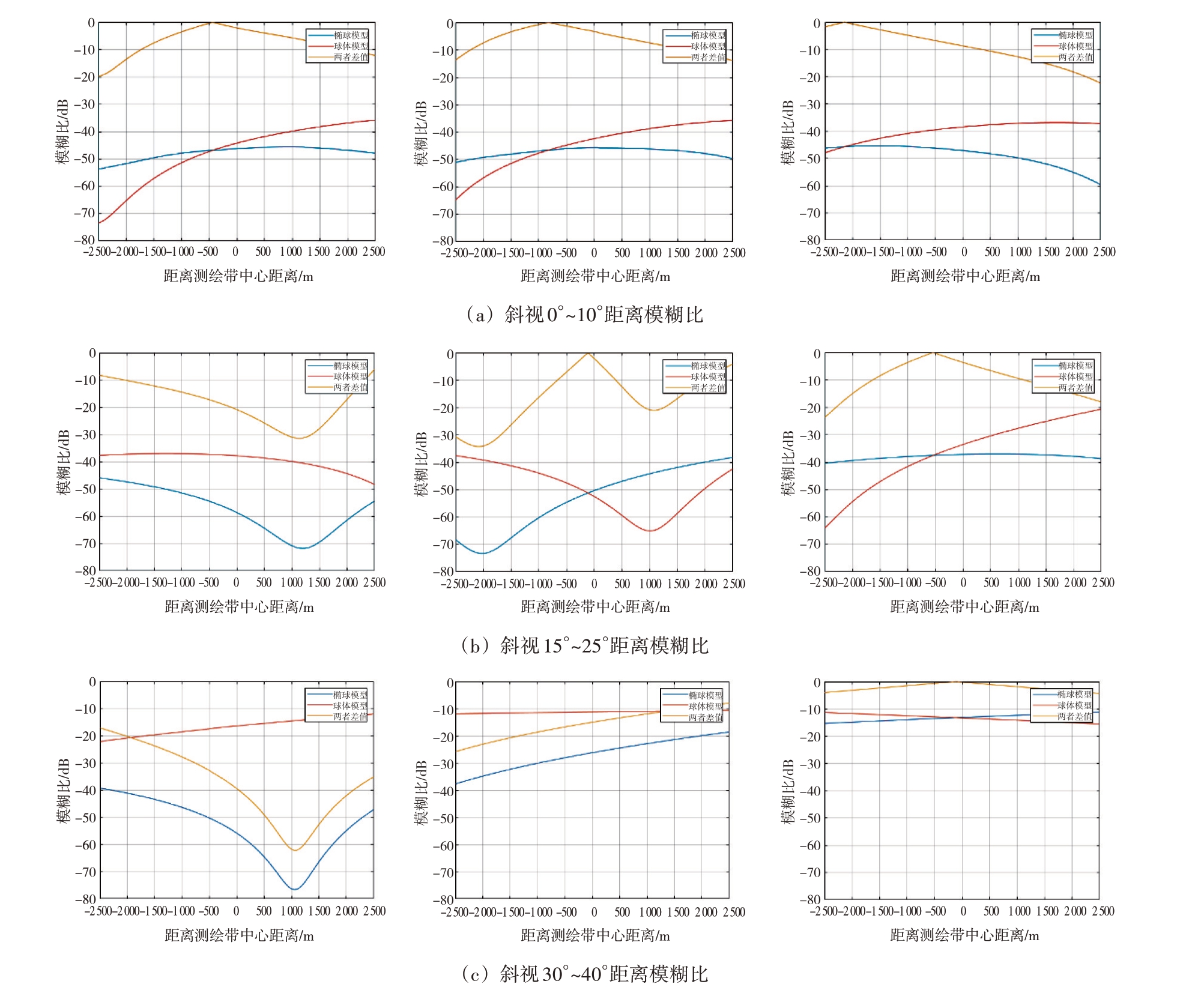
图7 PRF为5 000 Hz时距离模糊比曲线
由上图可见,在正侧视时两种模型下的距离模糊比差距很小,但随着斜视角不断增大,两者之间差异也随之增大;且距离模糊比也在不断增大,造成该现象的原因是在仿真过程中随着斜视角增大,卫星与目标点之间的斜距不断增大,由于波束宽度不变,使得模糊区越来越接近波束主瓣。示意图如图8所示。
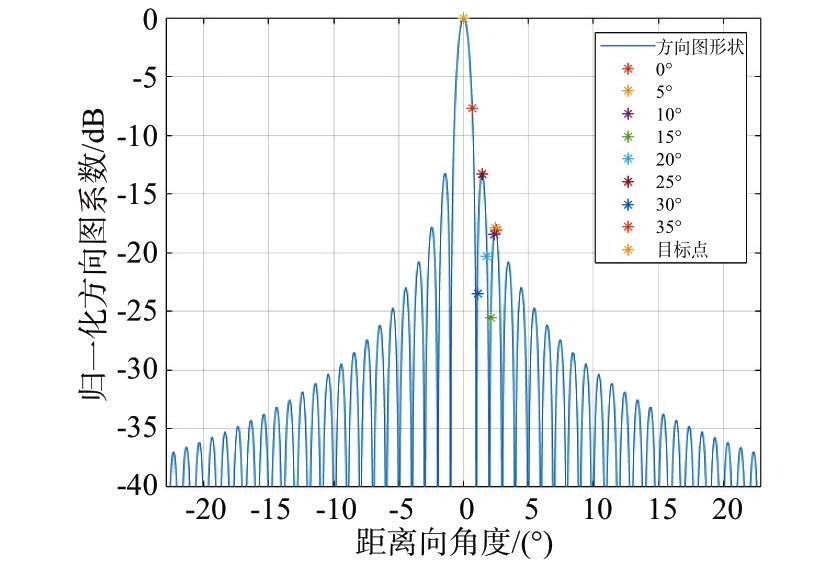
图8 不同斜视角第一模糊区在方向图中的位置
为了定量地比较球体模型与椭球模型下距离模糊比的差异,将两种模型的差异曲线进行均值化作为平均差值进行统计,同时对差异曲线上的最大差值也进行统计,结果如表2所示。
表2 距离模糊比对比 dB
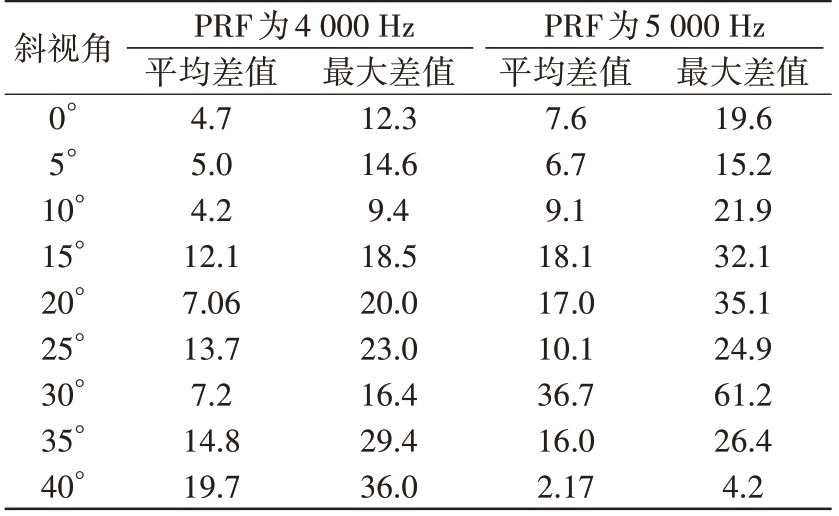
斜视角0°5°10°15°20°25°30°35°40°PRF为4 000 Hz PRF为5 000 Hz平均差值4.7 5.0 4.2 12.1 7.06 13.7 7.2 14.8 19.7最大差值12.3 14.6 9.4 18.5 20.0 23.0 16.4 29.4 36.0平均差值7.6 6.7 9.1 18.1 17.0 10.1 36.7 16.0 2.17最大差值19.6 15.2 21.9 32.1 35.1 24.9 61.2 26.4 4.2
从表2 可以看到,相同PRF 下,随着斜视角的增大,两种模型下的差异也逐渐增大,但也存在随着斜视角增大,两者之间差异减少的现象,分析原因如下:距离模糊比与模糊区在方向图中的位置相关,越靠近主瓣,旁瓣的峰值点越强,带来的模糊能量也会越强;但模糊区恰好处于主瓣附近的旁瓣零点附近时,模糊能量仍然较小。因此距离模糊比也呈现一定的无规律性。且越靠近主瓣,方向图的幅值变化越剧烈。
PRF为4 000 Hz的仿真结果,距离模糊比优于PRF 为5 000 Hz 的情况,符合距离模糊的变化规律。
由图7 可见,PRF 为5 000 Hz,斜视角为30°时,两者的距离模糊比差距非常大,现对场景中心的主要模糊区在方向图中的位置进行仿真绘图,其结果如图9所示。
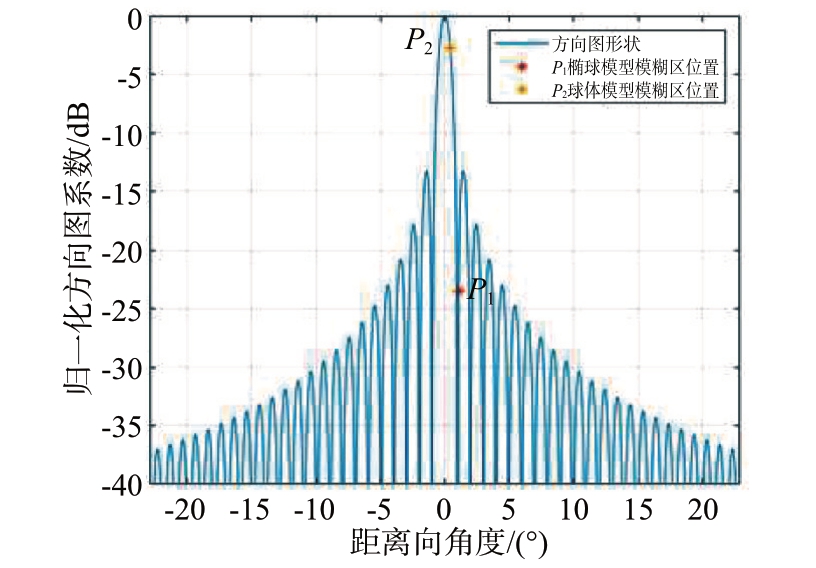
图9 PRF为5 000 Hz斜视角30°时两种模型模糊区所在位置
从图9可知,球体模型主要模糊区P2位于方向图主瓣,但椭球模型主要模糊区P1位于旁瓣,两者在方向图中的位置相差0.64°,但方向图系数相差20.8 dB,使得最终的距离模糊比差距较大。
2.2 距离模糊比沿方位向空变性仿真
在以往对距离模糊的仿真中,通常选用目标成像中心时刻的距离模糊比作为结果,但在一个合成孔径时间内,模糊区的位置会随着卫星位置的变化,发生相对应的改变,因此距离模糊比也存在一定的空变性。现对距离模糊的空变性进行仿真研究,仿真参数见表1,卫星工作模式选用条带模式,目标点取场景中心点,取点目标在方位向波束宽度内驻留的时间为合成孔径时间,因此斜视角不同,合成孔径时间不同。各斜视角下合成孔径时间如表3所示。
表3 不同斜视角下合成孔径时间
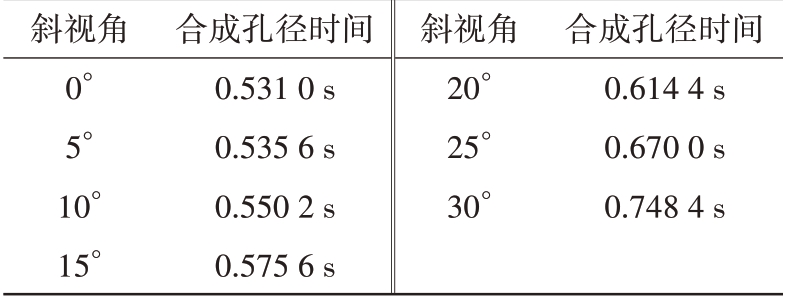
斜视角20°25°30°合成孔径时间0.614 4 s 0.670 0 s 0.748 4 s斜视角0°5°10°15°合成孔径时间0.531 0 s 0.535 6 s 0.550 2 s 0.575 6 s
以脉冲发射重复周期为时间间隔,仿真其在整个合成孔径时间内的距离模糊比,给出距离模糊比随合成孔径时间的变化曲线,不同斜视角下的结果如图10所示。
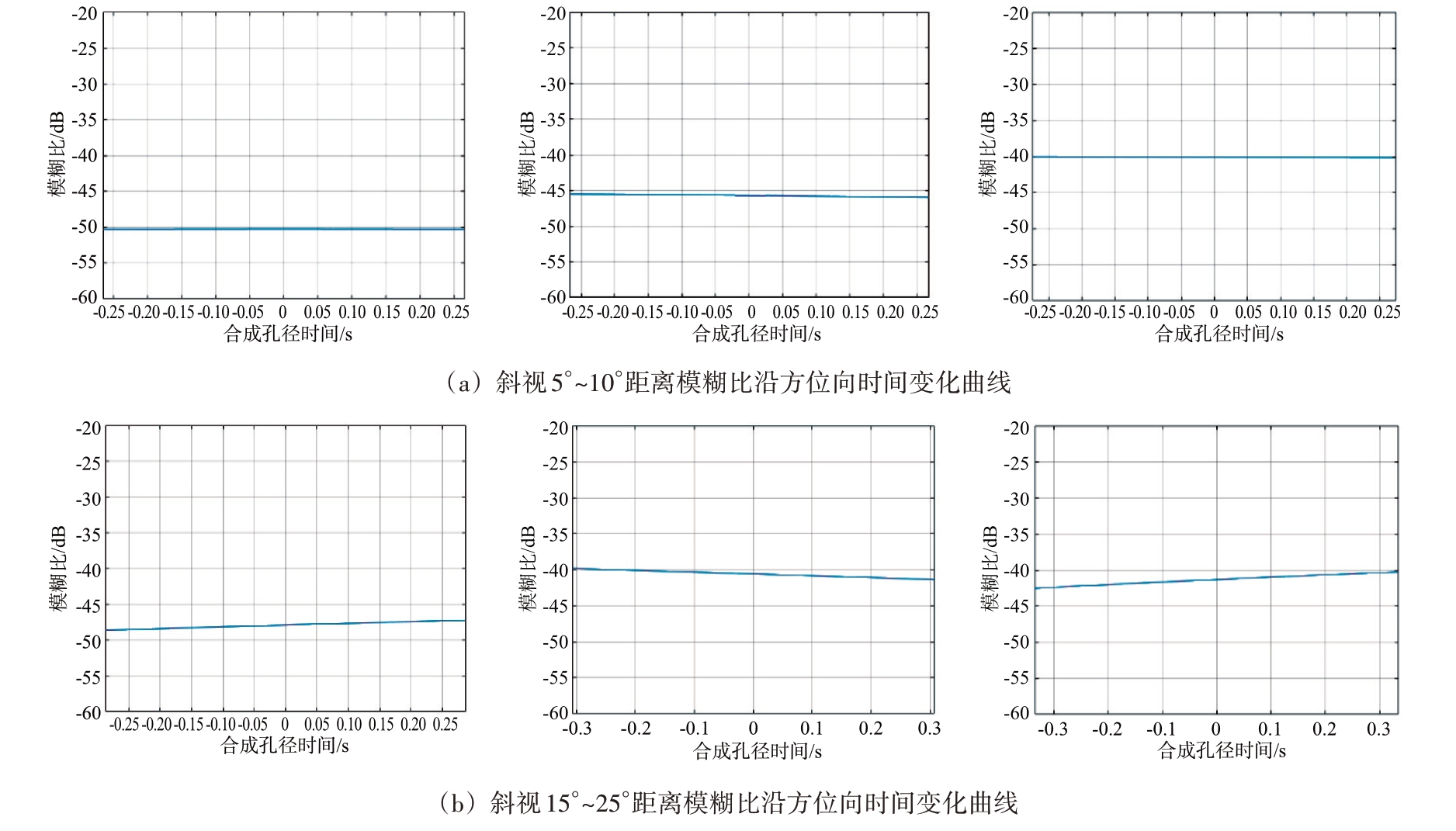
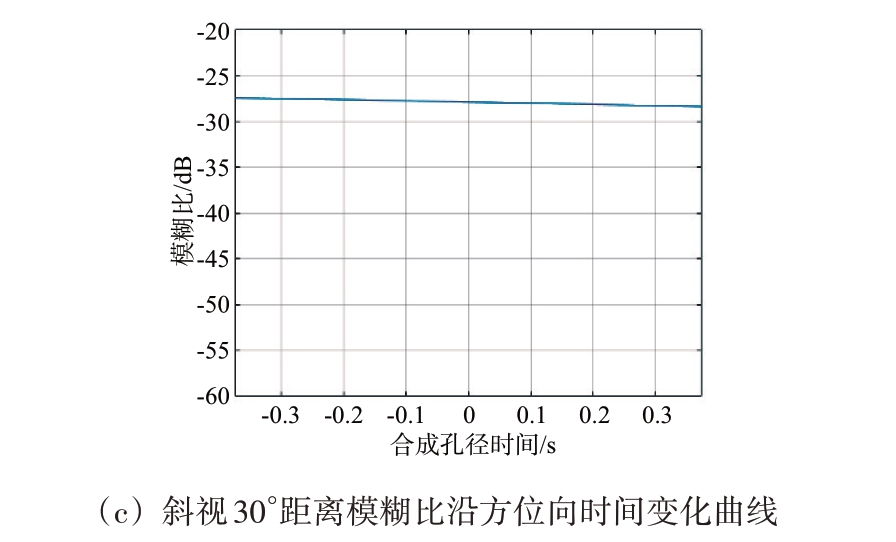
图10 不同斜视角下距离模糊比沿方位向时间变化曲线
统计不同斜视角下距离模糊比最大值、最小值以及两者的差值,如表4所示。
表4 不同斜视角下合成孔径时间内距离模糊比最大最小值
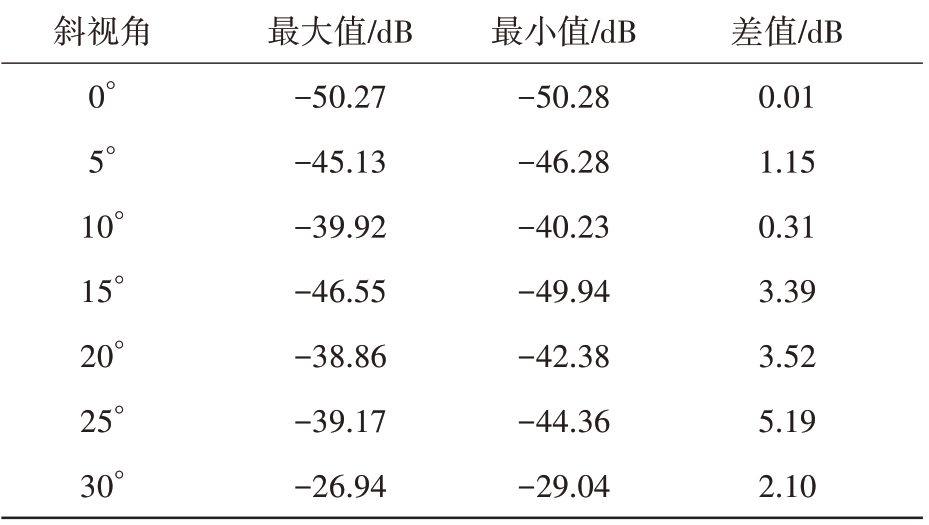
斜视角0°5°10°15°20°25°30°最大值/dB-50.27-45.13-39.92-46.55-38.86-39.17-26.94最小值/dB-50.28-46.28-40.23-49.94-42.38-44.36-29.04差值/dB 0.01 1.15 0.31 3.39 3.52 5.19 2.10
由表4数据可见,在正侧视时距离模糊比几乎没有变化,空变性较小,随着斜视角不断增大,距离模糊比在一个合成孔径时间内的差异也逐渐增大,空变性增强。
由于SAR 在不同工作模式下对天线波束的控制不同,因此距离模糊比在不同模式下也存在一定的差异性,利用表1中的参数,对条带模式、聚束模式、滑动聚束模式进行仿真对比,其中聚束模式和滑动聚束模式的分辨率选用0.5 m,不同斜视角下仿真结果如图11所示。
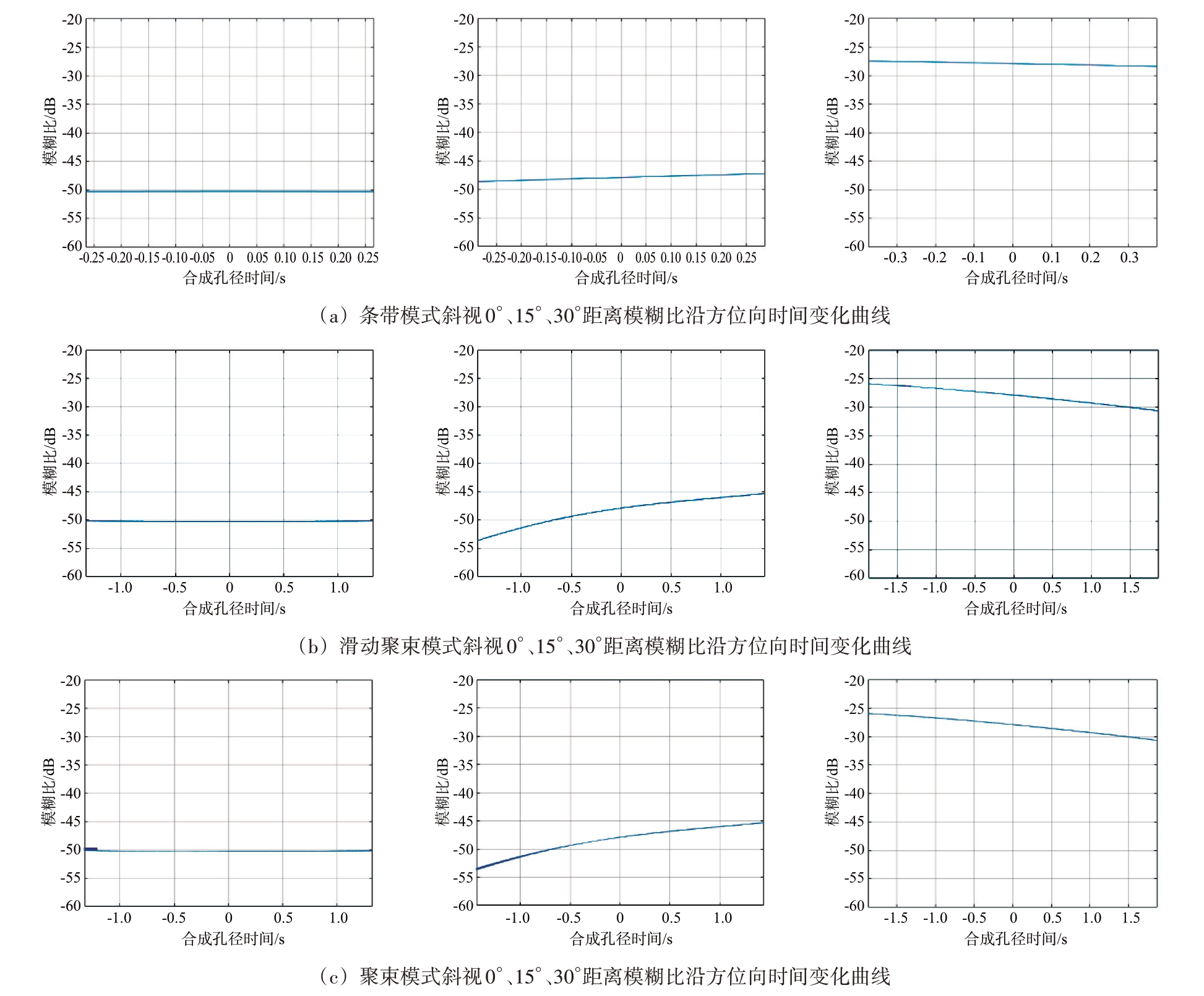
图11 不同模式下距离模糊比的对比
从图11 可以看到,滑动聚束模式和聚束模式下由于合成孔径时间的增长,距离模糊的空变性也随之增强,且聚束模式下在合成孔径时间边缘存在较大的波动性。
虽然距离模糊比存在一定的空变性,但在点目标成像能量累计过程中,距离模糊比应为整个合成孔径时间内总的模糊能量与总的信号能量的比值,定义为平均距离模糊比,公式如下:
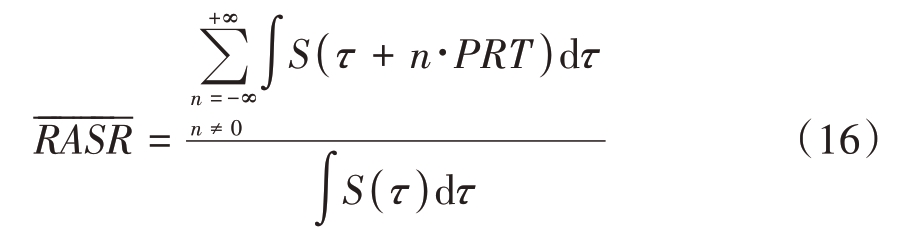
将条带模式下平均距离模糊比与点目标中心时刻的距离模糊比进行对比,分析距离模糊比受空变性的影响。对比结果如表5所示。
表5 中心时刻距离模糊比与平均距离模糊比的对比 dB
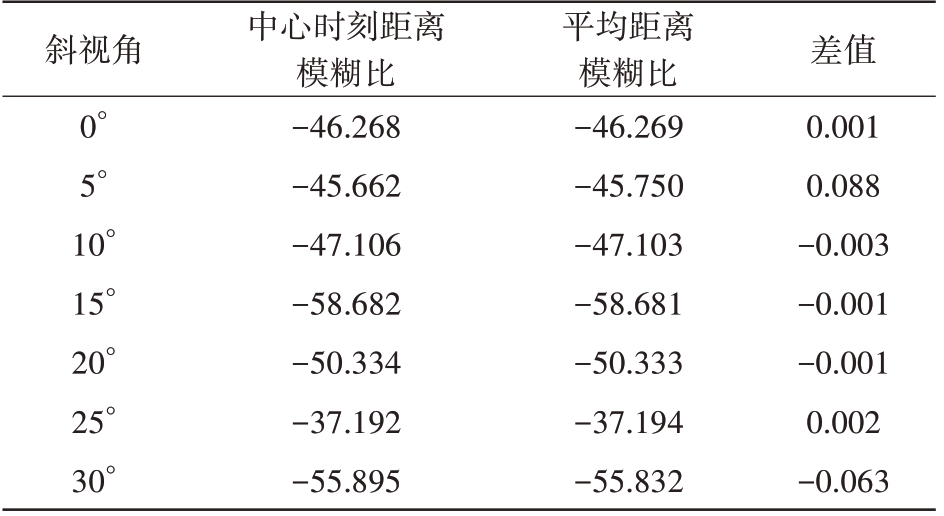
斜视角0°5°10°15°20°25°30°中心时刻距离模糊比-46.268-45.662-47.106-58.682-50.334-37.192-55.895平均距离模糊比-46.269-45.750-47.103-58.681-50.333-37.194-55.832差值0.001 0.088-0.003-0.001-0.001 0.002-0.063
由表5数据分析可得,在整个合成孔径时间内平均距离模糊比与中心时刻的距离模糊比差距很小,可以利用中心时刻的距离模糊比估计平均距离模糊比,简化距离模糊仿真评估过程。
3 结束语
本文在距离模糊计算中采用更精确的椭球模型取代传统的球体模型,使得距离模糊比的计算更加准确;通过构建斜视天线坐标系,利用改进的RD 定位算法计算模糊区位置,使计算过程更简单有效。并使用该方法对球体模型和椭球模型沿距离向测绘带的距离模糊比进行仿真对比,分析两者之间的差异,仿真结果表明两者差异与模糊区在方向图中的位置有关。本文还对距离模糊比的方位向空变性进行仿真分析,仿真结果表明距离模糊比沿方位向的空变性虽然会随着斜视角逐渐增大,但平均距离模糊比和中心时刻的距离模糊比相当,可以用中心时刻的距离模糊反映SAR 系统的性能。
本文的研究内容和仿真结果对星载SAR 系统设计具有重要参考价值,已用于某工程型号距离模糊计算。
[1]MEHLIS J G.Synthetic Aperture Radar Range-Azimuth Ambiguity Design and Constraints[C]// IEEE International Radar Conference, Arlington, VA, USA:[s.n.],1980:143-152.
[2]刘成,王华柯,全英汇,等.机载多载频频控阵非均匀距离模糊杂波抑制方法[J].系统工程与电子技术,2024,46(2):459-469.
[3]张永军,李彩萍.合成孔径雷达模糊度分析[J].电子与信息学报,2004,26(9):1455-1460.
[4]袁孝康.星载合成孔径雷达导论[M].北京:国防工业出版社,2005.
[5]CHEN Qi, HUANG Haifeng, YU Anxi, et al.A New Working Mode to Improve the Cross-Polarization Range Ambiguity to Signal Ratio[J].Chinese Journal of Radio Science, 2013, 28(6):1082-1087.
[6]邓云凯,禹卫东,张衡,等.未来星载SAR技术发展趋势[J].雷达学报,2020,9(1):1-33.
[7]MUFF D, IGNATENKO V, DOGAN O, et al.The ICEYE Constellation-Some New Achievements[C]//2022 IEEE Radar Conference,New York, NY, USA:IEEE, 2022:1-4.
[8]WANG Luanjing, ZHANG Shunsheng, WANG Wenqin.Range-Ambiguous Clutter Suppression for Forward-Looking FDA-MIMO Radar[J].Journal of Signal Processing,2022, 38(4):854-862.
[9]DONG Xichao, DING Zegang, WANG Jianping.Ambiguities in High Squint Mode SAR[C]// 9th European Conference on Synthetic Aperture Radar, Nuremberg,Germany:VDE, 2012:611-614.
[10]VILLANO M, KRIEGER G.Spectral-Based Estimation of the Local Azimuth Ambiguity-to-Signal Ratio in SAR Images[J].IEEE Trans on Geoscience and Remote Sensing, 2014, 52(5):2304-2313.
[11]DOGAN O, IGNATENKO V, VEHMAS R, et al.Reconsidering the SAR Range Ambiguity to Signal Ratio: Theoretical Analysis and Measurement Results[C]//2023 24th International Radar Symposium, Berlin, Germany:IEEE, 2023:1-10.
[12]郭艺夺,宫健.基于稀疏恢复的自适应角度多普勒补偿方法[J].雷达科学与技术,2020,18(5):517-523.
[13]杨汝良,李海英,李世强,等.高分辨率微波成像[M].北京:国防工业出版社,2013.
[14]黄丽佳.中高轨道SAR 成像算法研究[D].北京:中国科学院大学,2011.