0 引 言
认知雷达根据环境以及目标的变化自适应地优化发射波形,从而使雷达的性能保持在相对较高的水平[1-2]。因此发射波形的质量直接影响了认知雷达的性能[3-6]。波形设计的实质是通过改变发射能量的分配情况,最大化回波中探测任务的信息量。
Bell[7]首先提出最大化雷达目标和回波之间的互信息来设计发射波形的方法。文献[8]提出了一种基于信杂噪比(SCNR)和互信息(MI)的鲁棒波形设计方案,使得认知雷达在不利的环境中也可以获得相对较好的波形[9]。杨庆培将博弈论引入到雷达波形的设计中,以最大化互信息或信杂噪比建立效用函数,经推导双方存在纳什平衡[10]。文献[11]提出了一种使用卡尔曼滤波和最小化目标回波之间互信息的策略,来提高雷达检测概率。文献[12]提出了一种在SINR 约束下,基于最大化互信息的波形设计方法。
传统的波形求解方法往往受限于复杂的优化目标和约束条件,难以同时考虑多个因素的权衡。而智能算法则通过模拟生物进化、群体行为等机制,能够更灵活地搜索优化空间,实现多目标、多约束条件下的波形优化[13]。文献[14]提出利用一维卷积神经网络进行发射波形的设计,这种方法的优势在于可以通过神经网络学习复杂的波形模式,从而实现自适应波形设计。然而,这种方法需要大量的数据集进行训练,才能够达到良好的效果。文献[15]提出一种基于深度强化学习的频点自适应快速选取方法。利用深度强化学习的探索与反馈机制,从雷达与干扰机的持续对抗中学习和优化频点选取策略。迄今为止,已经提出并研究了许多进化多任务优化算法[16]。这些算法研究不同种群之间的知识重用,以更高效地求解多任务优化问题。现有的许多方法的思路是转移特定于任务的知识,例如将高质量的解决方案从一个任务转移到其他任务以增强优化能力。文献[17]提出了元知识转移算法,其通过转移在进化搜索过程中的知识,来促进种群向最优值方向前进。但是元知识的计算需要遍历种群的个体来计算质心,导致计算比较复杂,并且不能处理带约束的问题。
不同雷达任务之间存在耦合性,但是为了减少负转移给进化带来的危害,并处理雷达发射波形求解中存在的能量限制,本文提出了MKTC-ES算法。首次将元知识转移的方法应用到雷达多任务求解中来,在算法中通过转移协方差矩阵自适应进化策略(Covariance Matrix Adaptive Evolutionary Strategy,CMA-ES)的均值、标准差和进化路径来进行元知识的转移。将已经学习到的优化策略和信息迁移到新的雷达任务求解中。并且构建了自适应惩罚函数来解决发射波形能量约束。本文以MI 和SCNR 这两个雷达发射波形最常用的两个优化准则进行仿真实验。
1 雷达模型建立及分析
1.1 信号模型
基于信息论的多任务雷达最优发射波形设计研究旨在综合考虑多个目标探测任务,以提高雷达系统的综合性能。在这种研究中,每个任务之间被视为相互独立的,因此可以针对每个任务选择不同的优化准则进行分析和设计。通过这种方式,可以根据不同任务的特点和要求,定制相应的最优发射波形,以达到最佳的性能表现。当目标回波传输到达接收端后,由于同一个雷达系统的接收机滤波器结构是一致的,因此各个目标信道的噪声服从相同的统计特性。这一特性使得我们可以对目标信道的噪声进行统一处理,从而更有效地进行波形设计和性能优化。多任务雷达发射波形模型如图1所示。
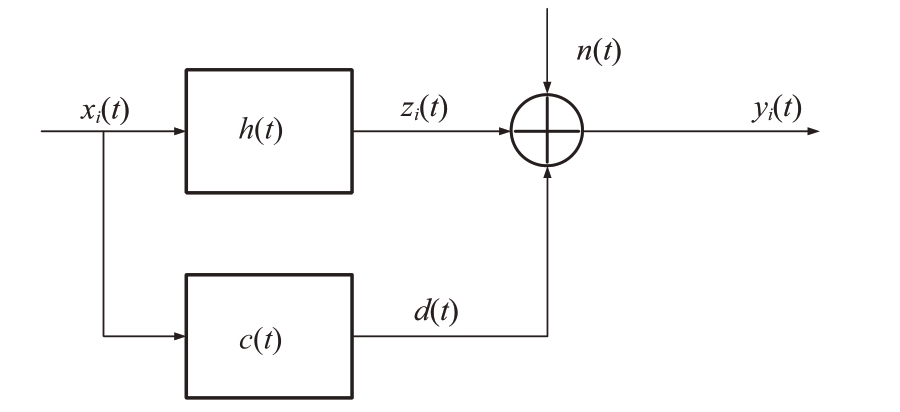
图1 多任务雷达发射波形模型
图中xi(t)是根据不同优化准则设计的发射波形目标函数,zi(t)是xi(t)和探测目标h(t)卷积之后的输出结果,![]() 。
。
假设给定K个雷达目标探测任务(不失一般性假设都是最大化问题),记为T1,T2,…,TK,其中任务TK 对应的搜索空间和目标适应度函数分别为SK和fK,多任务雷达波形设计是找到![]() 同时满足
同时满足
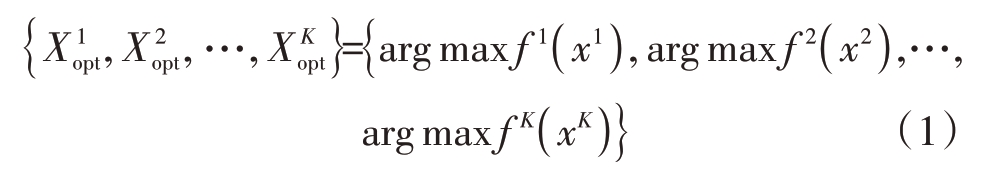
式中,![]() 分别是雷达探测任务T1,T2,…,TK的最优解。
分别是雷达探测任务T1,T2,…,TK的最优解。
根据优化准则推导出的目标函数一般可以作为目标适应度函数fK,而寻找到的满足任务的最优解![]() ,即为求解到的最优发射波形
,即为求解到的最优发射波形![]() 。
。
1.2 信号模型
本文要研究的互信息是目标h( t )与回波y( t)在已知发射波形x( t )情况下的互信息I(h( t ); y( t )|x( t ))。根据信息论的基本知识,可以得到Y与Z的互信息为
Z 是均值为0 的高斯随机过程,方差为![]() 。N是均值为0的高斯白噪声,均值为
。N是均值为0的高斯白噪声,均值为![]() 。D是与信号杂波相关的0 均值高斯随机过程,方差是
。D是与信号杂波相关的0 均值高斯随机过程,方差是![]() 。Y 是三者之和,由于它们都是统计独立的,所以Y 的方差
。Y 是三者之和,由于它们都是统计独立的,所以Y 的方差![]() 为
为
Y和Z之间的条件熵H( Y|Z )表示为
进而可得Y和Z之间的互信息为
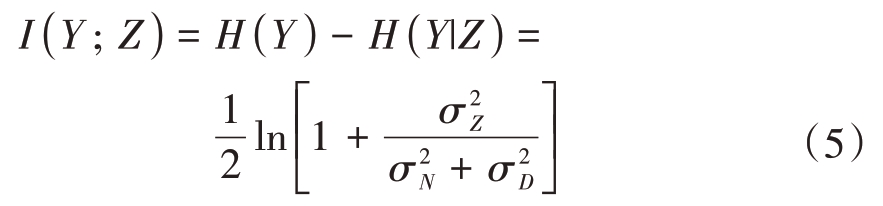
在假设每个信号可以用一系列均匀采样得到的样本替代时,我们考虑信号的能量均匀分布在这些独立同分布的采样点上。方差![]() 可表示为
可表示为

高斯白噪声在频率域内的功率谱密度![]() 是一个常数,可表示为
是一个常数,可表示为
同理可知每一个采样点上杂波过程的方差![]() 为
为

将上述![]() 和
和![]() 带入公式(5),互信息I( Y; Z )可表示为
带入公式(5),互信息I( Y; Z )可表示为
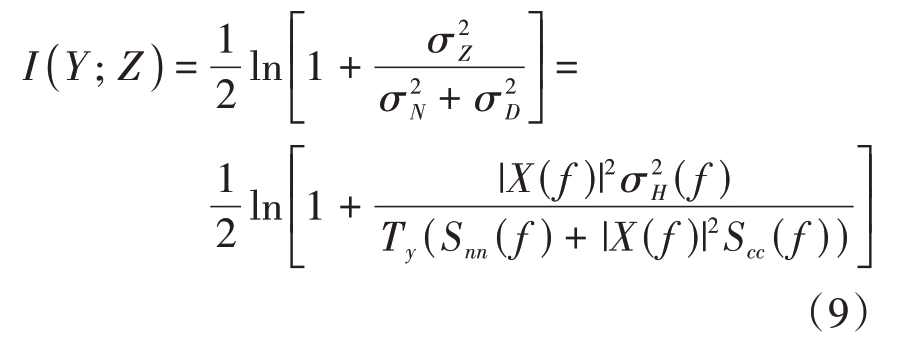
同样,设y( t )的频谱范围为[0,W],并将这个范围划分为多个互不相交的小区间,其中每个小区间的频率间隔为Δf。当Δf →0 时,即划分的小区间趋向于无穷小,互信息的表达形式则转化为积分形式。
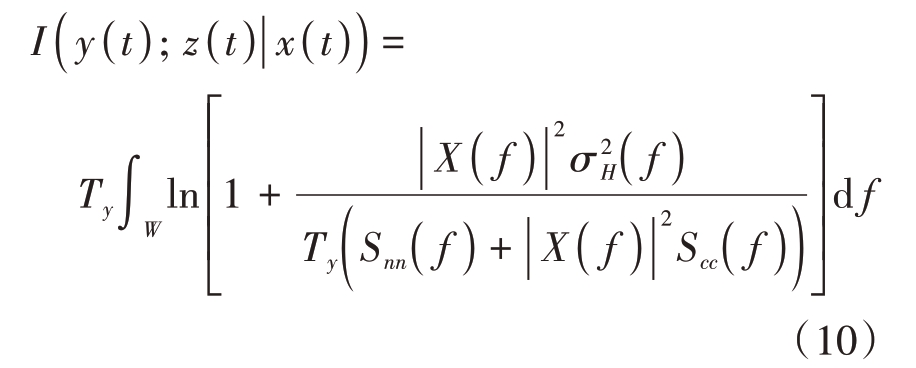
由于发射信号的能量是有限的,而且在有限能量的前提下又要将能量落在有效的带宽内,故能量约束为
因此,雷达发射波形优化问题转变成了以能量约束为条件,雷达回波与目标信号MI 表达式为目标函数的最优化问题,如下式所示:
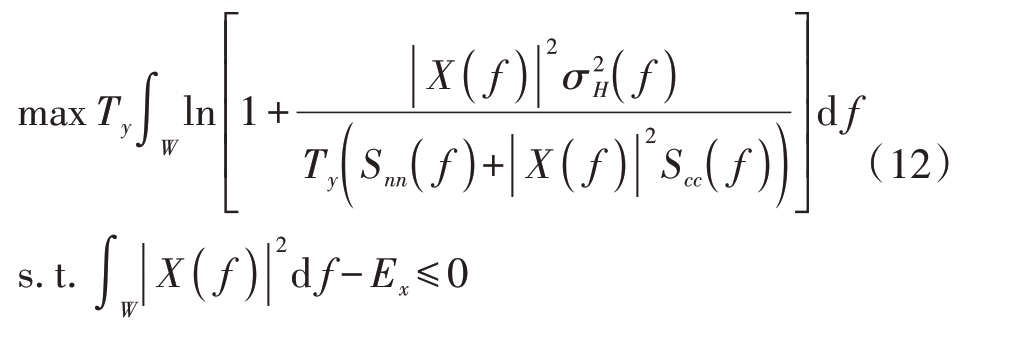
1.3 基于信杂噪比准则下的波形设计
根据雷达回波公式
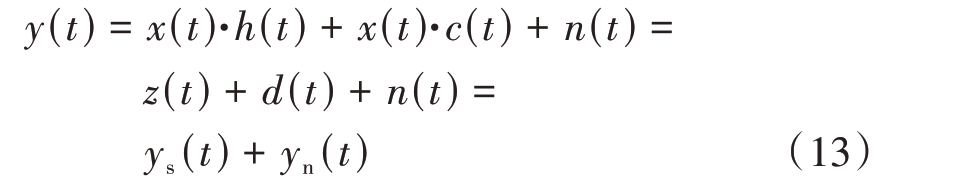
式中,ys(t)和yn(t)分别代表的是信号分量和干扰分量。
信杂噪比的定义是回波中有用的信号能量与干扰信号加噪声信号能量之比,因此
式中,
因此,
根据雷达发射能量约束,雷达发射波形优化问题转变成了以能量约束为条件,求雷达回波与目标信号SCNR 表达式为目标函数的最大值问题,如下式所示:
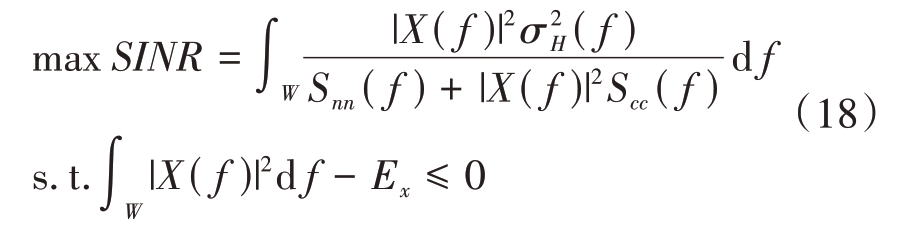
2 基于CMA-ES的PCMA-ES算法
CMA-ES 算法是目前最优秀的无导数寻优算法之一,其寻优过程有别于仅依靠随机性的交叉、变异操作来产生新子代,进行种群更新演化的传统进化算法。CMA-ES 算法以多元正态分布N(m,σ2C)的形式引导种群进化,协方差矩阵C 记录了连续步骤之间的累积依赖性,间接地控制着种群分布的“总体尺度”,从而使种群向着最优值存在的方向前进。与其他的进化算法相比,CMAES算法的参数设置、更新过程显得更加复杂一些。但在解决实际问题的过程中均值m 和均方差σ 的更新会加速算法的收敛速度,相较于更新协方差矩阵等参数消耗的时间可以忽略不计。
2.1 CMA-ES算法结构
CMA-ES 算法记录了一定迭代次数的种群历史,通过种群的进化路径来控制算法步长的大小。
2.1.1 新个体的产生
在CMA - ES 中,子代种群是通过采样N(m(g),(σ(g))2C(g))产生的。在第g 代新个体的产生公式如下所示:
其中N(0,C(g))是均值为0,协方差为C(g)的多元正态分布;![]() :第g+1 代中的第k 个子代;m(g) ∈Rn:第g 代搜索分布的均值;σ(g) ∈R+:第g 代的标准差。
:第g+1 代中的第k 个子代;m(g) ∈Rn:第g 代搜索分布的均值;σ(g) ∈R+:第g 代的标准差。
2.1.2 均值移动
新均值是根据新产生个体的适应度值进行移动的,从![]() ,…,
,…,![]() 中选取最优秀的u 个,然后使用加权平均产生新的m(g +1)。
中选取最优秀的u 个,然后使用加权平均产生新的m(g +1)。
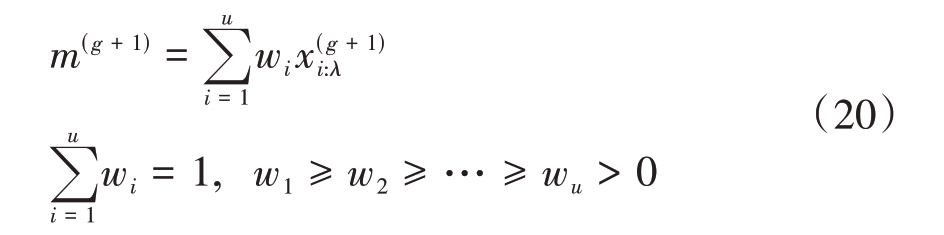
其中:u ≤λ为父代种群的大小,每一代选择最优的u 个子代;![]() 是新产生种群各体中的第i 个最优的个体。
是新产生种群各体中的第i 个最优的个体。
2.1.3 自适应协方差矩阵的更新
为了摆脱协方差矩阵对种群大小的依赖,CMA-ES 算法不仅仅使用从单代中所有选择的步,从零开始估计完整的协方差矩阵。而是独创性地使用了秩1和秩μ相结合的方式进行更新。秩1更新中的进化路径会利用移动步长的符号信息和连续步骤之间的相关性,在小种群时非常的有效。而秩μ更新则是额外使用前几代的信息,从零开始估计了完整的协方差矩阵,这在大种群中非常有效。而协方差矩阵C 采用秩1 和秩μ 相结合的方式进行更新,这样既保证了搜索的速度,又保证了协方差矩阵的可靠性。协方差矩阵的更新为
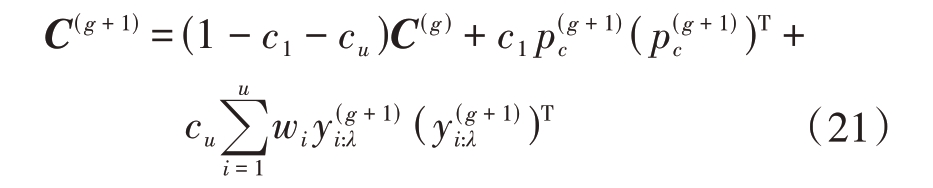
式中:![]() 代 表 第g 代 的 进 化 路 径;
代 表 第g 代 的 进 化 路 径;![]()
![]() 。
。
2.1.4 步长控制
进化路径可以看做是一系列子步的和,可以通过控制进化路径的“长、短”,来控制搜索步长的大小。共轭进化路径可以写为
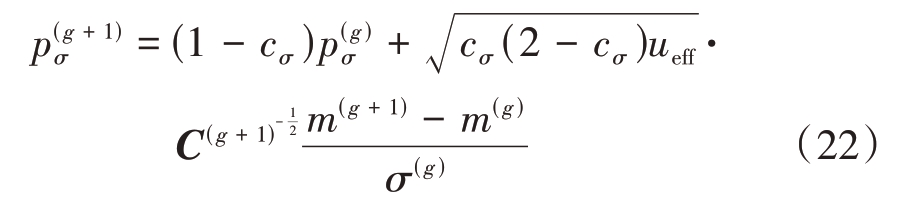
式中:![]() 为第g 代的共轭进化路径;
为第g 代的共轭进化路径;![]() 为归一化常数;
为归一化常数;![]() 。
。
将进化路径的长度![]() 与随机选择下的期望长度E||N(0, Ι)||进行比较。在随机选择下,连续的步骤是独立的,因此是不相关的。所以可以根据比较的结果来改变σ的大小,步长σ(g)可以写为
与随机选择下的期望长度E||N(0, Ι)||进行比较。在随机选择下,连续的步骤是独立的,因此是不相关的。所以可以根据比较的结果来改变σ的大小,步长σ(g)可以写为
2.2 自适应惩罚函数与适应度函数结合
在求解认知雷达最优发射波形x( t )时,必须考虑能量约束,确保发射波形的能量不超过特定阈值Ex。这些约束条件限制了波形的设计空间。如果直接将CMA-ES 算法应用于带有约束条件的优化问题,可能会导致生成的解不满足约束条件。为了克服这一问题,本文提出了一种创新的PCMA-ES 算法,将自适应惩罚函数方法与CMA-ES 算法相结合。相较于传统的死亡惩罚函数和动态惩罚函数,自适应惩罚函数方法能够根据当前种群中可行解的比例自适应地调整惩罚系数,更灵活地挖掘不可行解的信息,逐步接近最优解。
首先,我们需要明确区分在能量约束下的两个种群:可行解种群和不可行解种群,并为它们定义不同的适应度函数。以互信息优化准则为例,适应度函数f( x )的定义为
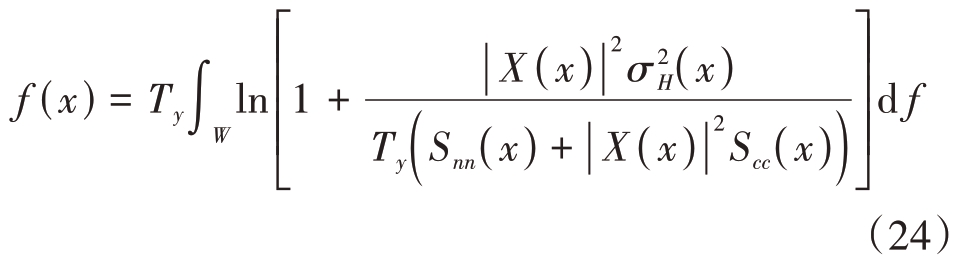
将可行解中适应度最优的目标函数值记为bestfeas,则自适应惩罚适应度函数可表示为
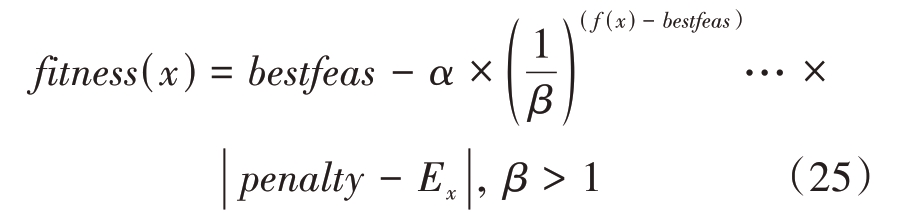
式中:参数α、β 为自行设定的参数;penalty 为当前种群分配能量的总和;Ex为发射波形的总能量。
CMA-ES 算法在每次迭代中选择优秀的父代个体时,不再直接比较每个种群的适应度值,而是采用新的适应度函数进行替代。这个新构建的自适应惩罚适应度函数fitness(x)中,根据违反约束的程度和适应度值对不可行的解进行自适应的惩罚,惩罚值会根据总体中所有解的约束违反情况在几代中进行更新。由于在自适应惩罚适应度函数中bestfeas 代表了可行解最佳的适应度值α ×![]() 。
。
因此任何的不可行解决方案都将受到惩罚,其适应度值会低于最优的可行解。这种机制能够有效利用不可行解中的有效信息,甚至使得不可行解的适应度值可能比没有违规的可行解更高。但是,任何不可行的解决方案都不能比总体中最佳可行解决方案有更高的适应度值。
3 MKTC-ES算法
多任务雷达模型的核心思想是综合考虑多个任务之间的关系和相互影响,以及任务之间的优先级和权衡关系,通过合理分配有限的资源,使得雷达系统在多个任务之间能够实现有效的协同和优化。多任务雷达波型设计的关键在于开发一种用于求解多任务雷达发射波形的算法。这种算法需要能够同时考虑多个任务的需求,并在有限的资源条件下进行有效的优化。通过合理地分配有限资源,如发射能量和带宽,该算法能够使得雷达系统在不同任务之间实现平衡和优化,从而提高雷达系统的综合性能和适应性。
3.1 元知识转移
MKT 方法旨在传递元知识以改进所有群体中解决方案的生成,从而更有效地解决多任务求解问题。
在给定任务k后,![]() 和
和![]() 是第g代和g+1代中获得的任意特定于任务的知识(例如,解决方案)。其中i 是个体索引,
是第g代和g+1代中获得的任意特定于任务的知识(例如,解决方案)。其中i 是个体索引,![]() 具有比
具有比![]() 更好的适应度,第g代的元知识是rk, g。
更好的适应度,第g代的元知识是rk, g。![]() 可以表示为
可以表示为
式中,⊕表示任何合适的运算。
由于高质量的解决方案是基于人口分布信息(指的是通过适应度函数对种群中个体的表现进行评估后得到的统计信息)生成的,因此我们通过传递人口分布信息来实现MKT。而CMA-ES 算法的人口分布信息可以使用均值和方差进行表示,从式(21)和(22)中可以看出进化路径在协方差矩阵C 和步长σ(g)的更新中具有重要的作用,而根据式(19)可知协方差矩阵C 和步长σ(g)直接决定了新个体![]() 的生成。
的生成。
由于rk,g 是根据其对应种群P 中的个体计算的,因此我们可以将源种群中的个体转移到转移种群中,然后将转移种群与目标种群融合,以产生更合适的![]() 。可以将转移群体Ptr 和目标群体pt的信息关联为融合群体pf:
。可以将转移群体Ptr 和目标群体pt的信息关联为融合群体pf:
通过这样做,pf 将获得来自目标任务的群体(即pt)和从源任务转移的群体(即从ps 获得的Ptr)的进化信息,即进化有前途个体的元知识)。
基于此考虑和式(19),可得到转移种群的新个体为
简单地说,知识迁移就是从Ps 和Pt 中计算出m(g +1)、σ(g +1)、进 化 路 径![]() 。之 后 根 据
。之 后 根 据![]() 的大小与方向来指导Ps和Pt的数据融合以生成Pf。之所以是使用pc 和pσ 来指导种群的融合,是因为进化路径直接控制步长的大小。即直接指明了种群的进化方向,指向了进化出高质量解决方案的方向。
的大小与方向来指导Ps和Pt的数据融合以生成Pf。之所以是使用pc 和pσ 来指导种群的融合,是因为进化路径直接控制步长的大小。即直接指明了种群的进化方向,指向了进化出高质量解决方案的方向。
算法1给出了相应的伪代码,详细描述了元知识迁移和融合的过程。MKTC-ES 算法的核心是通过迁移源任务的元知识(进化路径、均值、方差等)优化过程的信息,到目标种群形成融合种群。将这些元知识应用到目标任务的优化过程中,加速目标任务的优化过程。在融合种群中,源任务的元知识可以用来初始化目标任务的个体,或者通过调整目标任务的个体来适应源任务的特性。这样,在优化过程中,目标任务的个体可以借鉴源任务的经验和信息,从而更快地找到最优解。同时,融合种群也会在优化过程中不断地调整和更新,以适应目标任务的变化和需求。
算法1 元知识转移

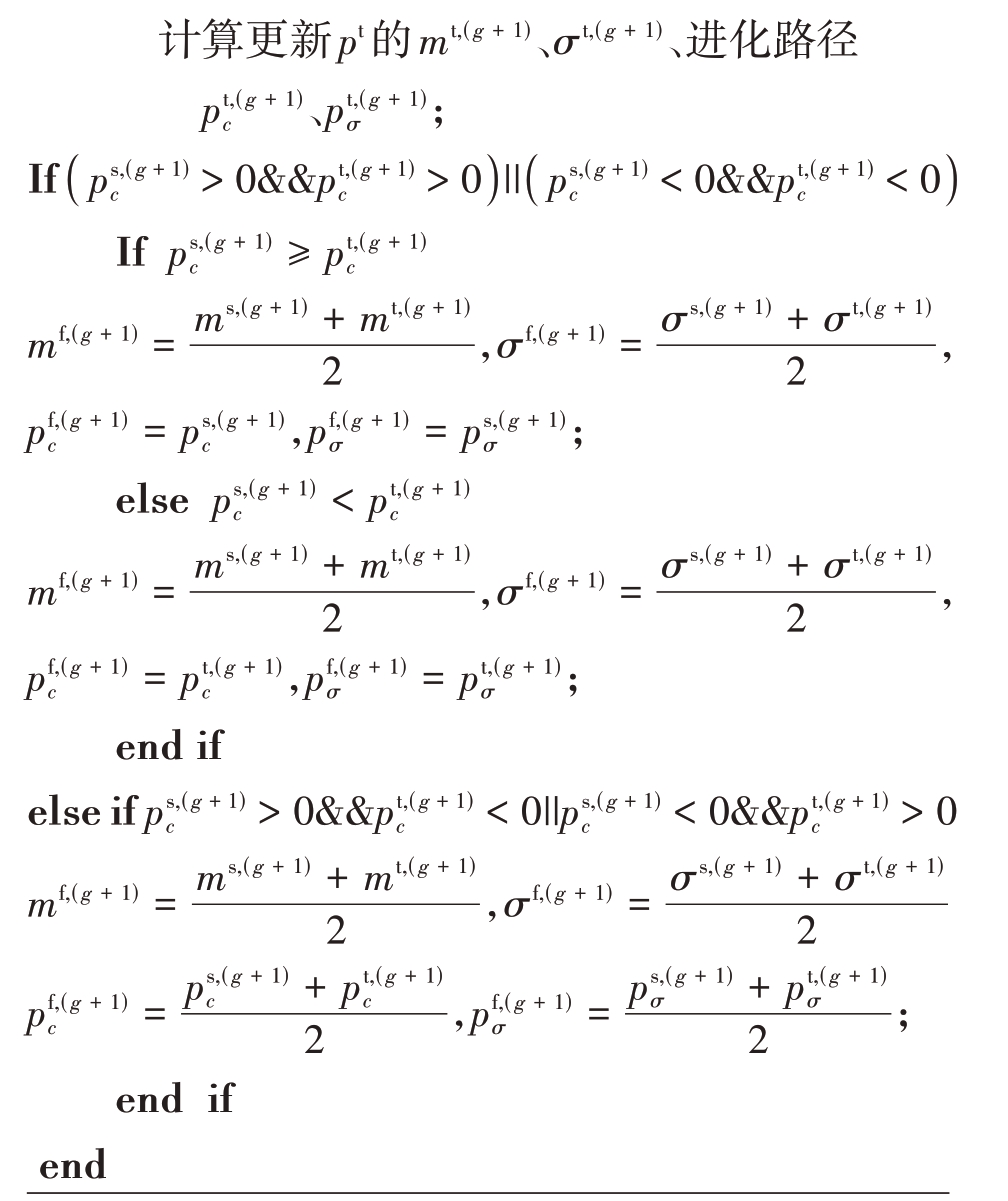
本文在元知识迁移过程的创新之处,在于结合了源任务的进化路径信息以及目标任务的优化需求,通过指导源任务的元知识和目标种群的融合过程,实现了更加智能化的迁移过程。具体来说,根据源任务的进化路径的方向和大小,可以灵活地调整源任务的元知识和目标种群的融合情况,以适应目标任务的优化需求。如果源任务的进化路径指向一个与目标任务相似的优化方向,即pt和ps的进化路径的方向符号一致,那么采取更加积极的方式将源任务的元知识融合到目标种群中,以加速目标任务的优化过程。相反,如果源任务的进化路径与目标任务的优化方向相差较远,即pt和ps的进化路径方向符号不同,那么可以适度地调整源任务的元知识和目标种群的融合情况,以平衡源任务和目标任务的影响,避免对目标任务的优化产生不利影响。
3.2 精英解决方案转移
除了MKT 之外,还提出了精英解决方案转移(Elite Solution Transfer, EST)来改善优化结果。EST的思想是在不同群体之间转移精英解决个体,以帮助其进化来解决不同的任务。雷达任务的全局最优解在某些维度上必定具有相似性(无论什么类型的雷达任务,它们总是会尽量避开杂波的干扰),这有利于种群之间的知识转移。但是如果不同任务的最优值相差很大,可能导致负知识转移,从而误导进化。因此,为了避免这种限制并确保知识转移能够提高种群质量,EST中设计并采用了一种简单但有效的标准来控制转移。具体来说,Ps 中的精英解个体只有当其适应度优于Pt 中的最差个体时,才会转移到Pt。然后,Pt 中最差的个体被这个精英解个体取代。否则,精英解将不会被转移。这样做可以保证知识转移是积极的,因为转移后目标人群的平均适应度肯定会比转移前更好。
3.3 完整的MKTC-ES算法
本部分详细介绍了为解决多任务优化问题而开发的MKTC-ES 算法,它基于MPMT(Multiple Populations for Multiple Tasks)框架,即为每个任务分配一个种群,并行解决多个任务。在算法求解过程中使用元知识迁移策略和精英解决方案的方法保证算法性能。另外,MKTC-ES 算法还通过构建自适应惩罚函数法与CMA-ES 算法相结合的方式,使得算法能够在优化过程中解决能量约束问题,从而保证生成的解满足雷达任务的能量限制要求。
综上所述,MKTC-ES 算法在多任务雷达优化问题中,通过多种策略和方法的结合,能够充分考虑任务之间的相关性和共享信息,同时解决雷达任务的能量约束问题,从而实现对多个任务的同时优化。算法2 给出了使用MKTC-ES 求解MI 和SINR优化准则相应的伪代码。
算法2 MKTC-ES求解多任务


4 仿真实验
本文首先仿真验证了所提出的自适应惩罚函数法与CMA-ES 算法相结合的PCMA-ES 算法,可以求解出存在能量约束的MI(SCNR)优化准则的最优发射波形。之后验证了所提出的MKTC-ES算法可以求解多个雷达任务。为了显示所提出算法的有效性,还采用了一些最先进的性能良好的MFEA 算法进行比较。算法设置均与原始论文保持一致。为了减少统计误差,每个算法在问题上独立测试20 次,并使用平均结果进行比较。在仿真过程中噪声的功率谱密度Snn( f)是高斯随机白噪声,其值为1。设置初始频率f0和终止频率f1,信号频率的范围选取[-0.5,0.5],采样点数为256,发射波形的能量范围为[1,10]。杂波表达式是一个混合余弦函数:

4.1 求解最优发射波形
图2展示了在杂波存在情况下,目标能量谱和杂波功率谱的分布图。图3 则展示了在杂波环境中,基于互信息优化准则,使用注水算法和PCMAES 算法求解出的最优波形。从图中可以观察到,最优发射波形的能量主要集中在0.1、0.2 和0.3 频率附近。
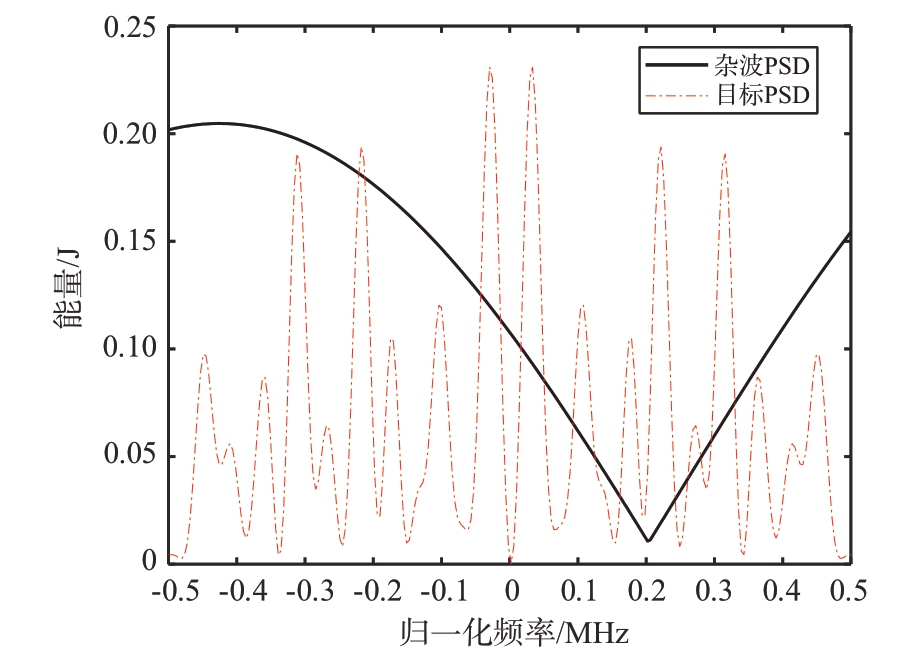
图2 目标谱与杂波功率谱密度
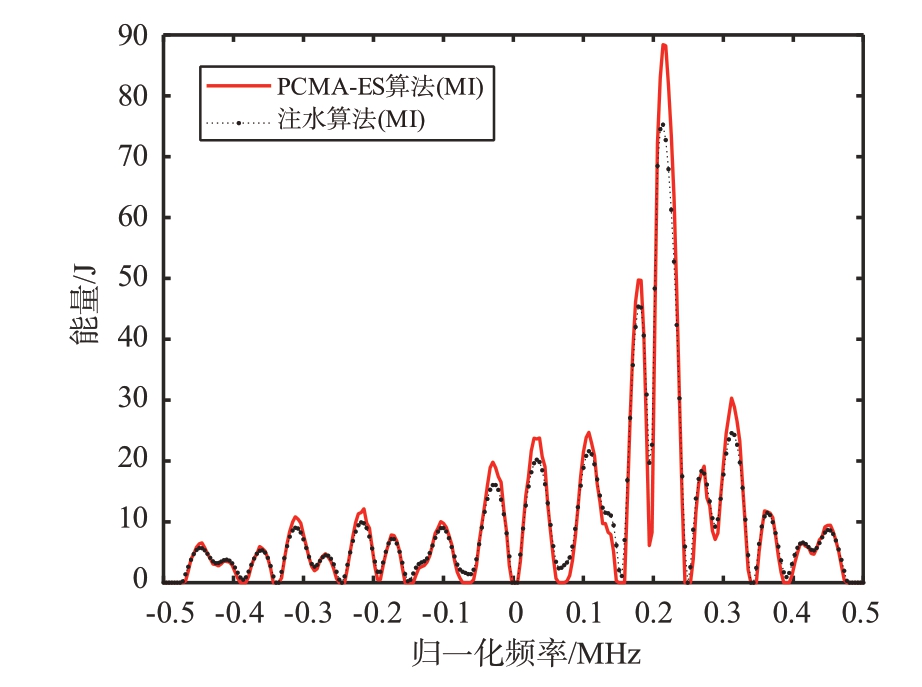
图3 基于互信息准则的最优发射波形
图4 为在杂波环境中,基于SCNR 优化准则,使用注水算法和PCMA-ES算法求解最优波形。从图中可以看出使用PCMA-ES算法和注水算法求解的最优发射波形在能量分布上趋于一致。它们都在杂波较小的频带内分配了更多的能量,在目标密度大但杂波也较大的频带内分配了较少的能量。这证明了本文提出的约束进化算法可以有效用于在杂波环境下求解最优发射波形。
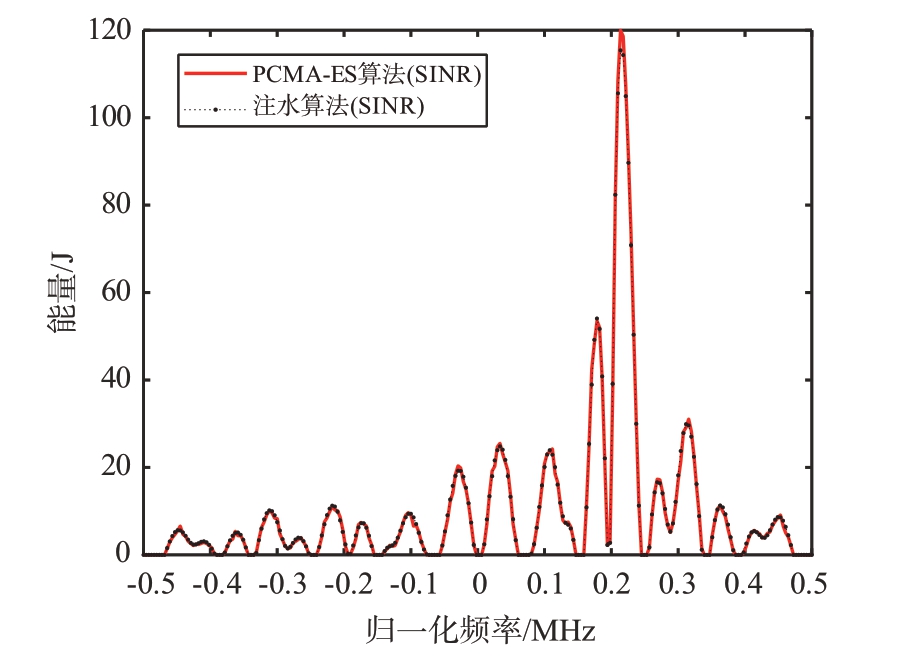
图4 基于信杂噪比准则的最优发射波形
图5是使用MKTC-ES算法同时求解出基于MI和SINR 任务发射波形仿真图,从图中可以看出基于MKTC-ES算法同时求解出多个雷达任务的最优发射波形。在考虑了两个任务的情况下,所得到的最优发射波形能够在平衡互信息和信干噪比之间达到较为理想的状态。这种结果表明MKTC-ES算法能够有效地处理多个任务的优化问题,并找到在多个任务指标之间取得较好平衡的最优解。在该图中,可以清晰地看到所得到的波形在保证目标信息传输的同时,也考虑了环境干扰的影响,使得雷达系统在复杂场景下具有更好的性能表现。
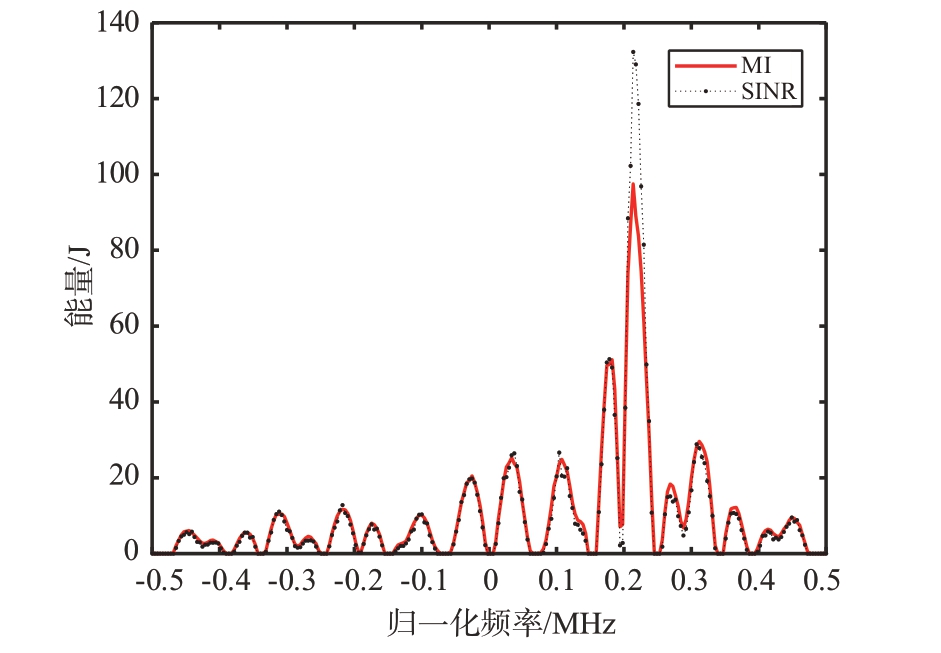
图5 使用MKTC-ES算法同时求解MI和SINR优化准则最优发射波形
4.2 MKTC-ES算法的性能仿真
通过对比图6 和图7 在1~10 能量范围下,MKTC-ES 算法和注水算法所得到的发射波形中包含的互信息或信干噪比值,可以了解MKTC-ES 算法在雷达最优发射波形设计中的优越性。MKTCES算法作为一种元知识转移和约束优化相结合的演化算法,在处理雷达波形设计问题时具有独特的优势。首先,MKTC-ES 算法能够充分利用元知识的转移,即通过将已经学习到的知识和经验应用于新问题的求解中,从而更好地探索和利用搜索空间中的信息。这种元知识的转移使得MKTCES 算法在解决高维度、复杂的优化问题时更加高效和灵活。其次,MKTC-ES 算法在约束优化方面也表现出色。在雷达波形设计中,通常需要满足一系列约束条件,例如能量分配范围、波形形状等。MKTC-ES 算法通过有效的约束处理方法,能够确保所得到的发射波形满足各项约束条件,从而提高了系统的稳定性和可靠性。通过对比实验结果,可以明显观察到MKTC-ES 算法相较于传统的注水算法在性能上表现更加优越。MKTC-ES 算法所得到的发射波形中包含的互信息或信干噪比值明显高于注水算法,这表明了MKTC-ES 算法能够更好地优化发射波形,使其在受到杂波干扰的环境中获得更好的性能表现。MKTC-ES 算法在雷达最优发射波形设计中展现出了明显的优势,其高效的元知识转移和优化约束处理能力为雷达系统的性能提升提供了可靠的技术支持。
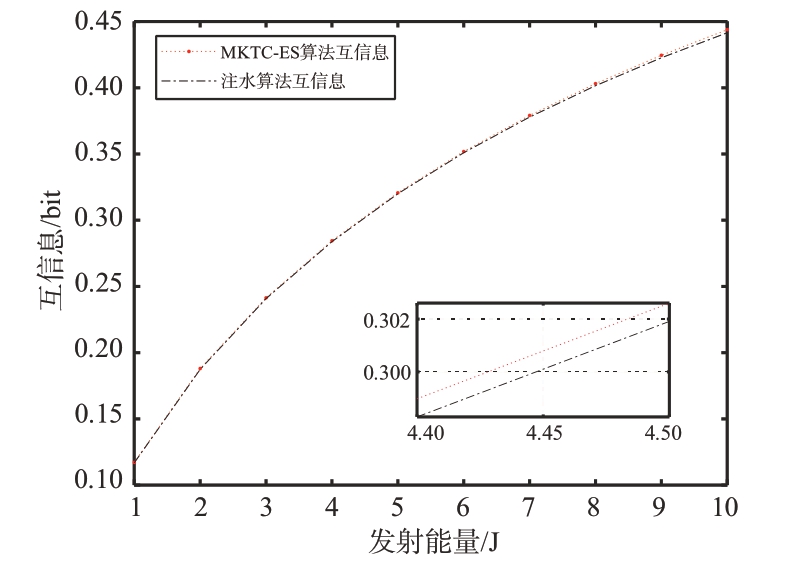
图6 基于MKTC-ES算法的波形互信息值比较
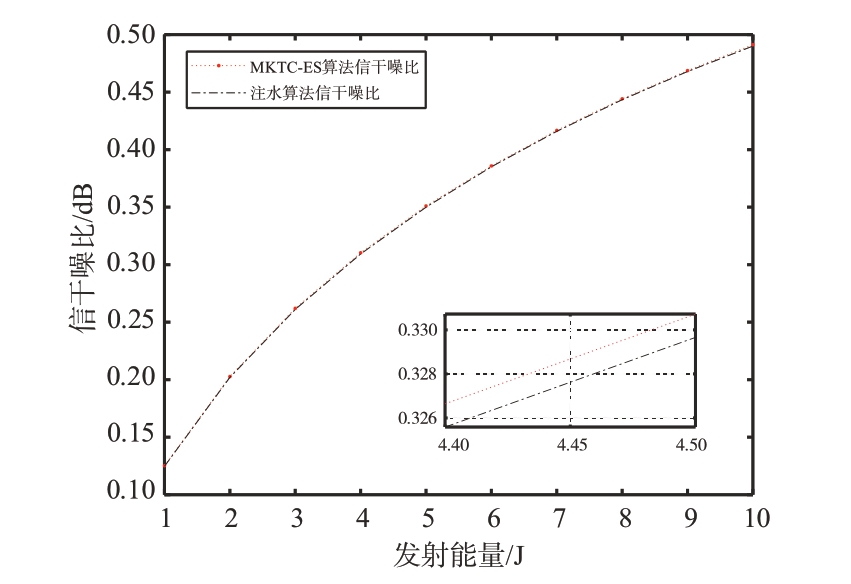
图7 基于MKTC-ES算法的波形信杂噪比值比较
图8 为使用MKTC-ES 算法同时进行互信息优化准则和信干噪比优化准则的自适应雷达最优波形的求解情况,以及单独使用PCMA-ES 算法求解MI优化准则和SINR 优化准则波形时,在每次迭代更新时最佳适应度值曲线的变化。从图中可以清楚地观察到,MKTC-ES 算法相较于单独的PCMAES 算法能够更快地寻找到最优发射波形,即其收敛速度更快。使用MKTC-ES 算法求解MI 和SINR优化准则的最优波形大约在第29代左右就能够找到。而单独使用约束进化算法则需要在第60到70代之间才能达到最优波形。此外,从最终的最佳适应度值来看,使用MKTC-ES 算法相较于单独使用PCMA-ES算法表现出更好的性能。这直接证明了在求解多个雷达任务时,进行元知识的转移可以有效促进每个雷达任务的求解。
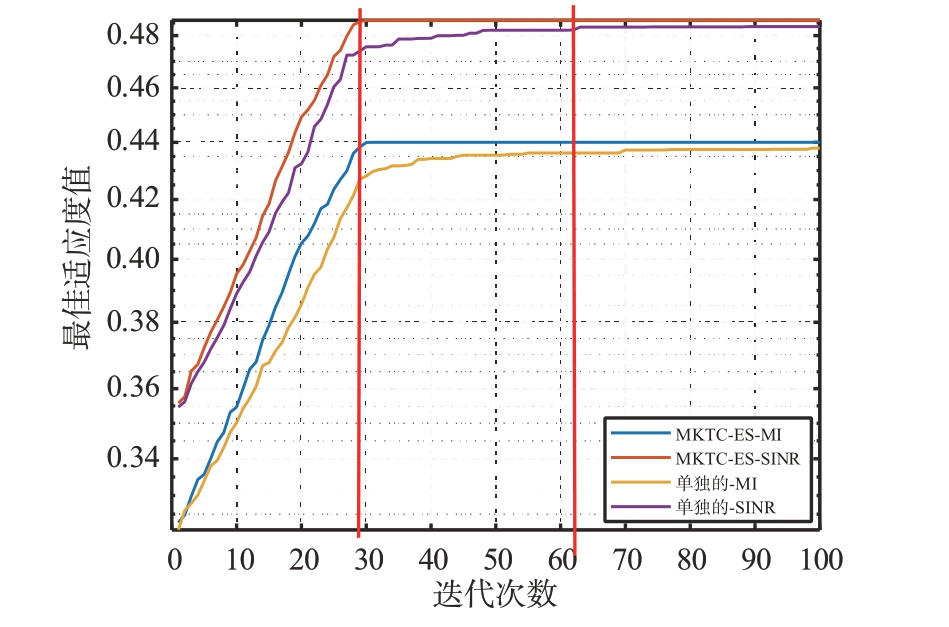
图8 使用MKTC-ES进行多任务求解和单独求解雷达任务算法上升曲线
表1 为使用MKTC-ES 算法和经典多任务算法MFEA 求解MI 和SINR 优化准则自适应雷达任务的性能情况。
表1 比较MKTC-ES和MFEA算法的性能
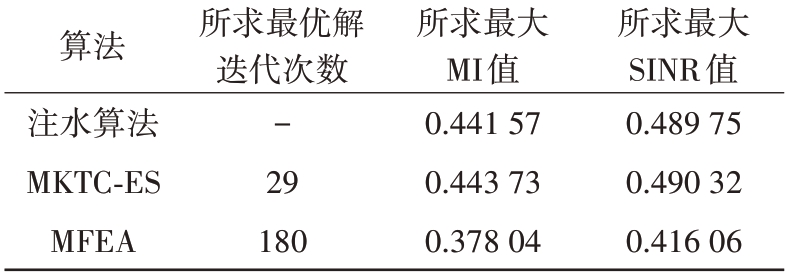
算法注水算法MKTC-ES MFEA所求最优解迭代次数-29 180所求最大MI值0.441 57 0.443 73 0.378 04所求最大SINR值0.489 75 0.490 32 0.416 06
从表中可以清晰地看出,MFEA 算法在处理雷达任务时表现不佳。尽管本文对MFEA 算法进行了优化,并采用了与MKTC-ES 算法相同的约束处理方法,但是由于MFEA算法本身在处理高维度问题时存在一定的局限性,因此其效率较低。雷达任务通常涉及到高维度的优化问题,MFEA 算法在处理高维度问题时往往需要更多的迭代次数才能找到满意的解,这导致了其相对较慢的收敛速度。
此外,从表中的结果可以看出,MFEA 算法所求得的MI 和SINR 波形与MKTC-ES 算法相比存在较大差距。这可能是由于MFEA 算法在多目标优化中的搜索策略不够有效,无法充分地探索和利用搜索空间中的信息。相反,MKTC-ES 算法通过引入元知识的转移策略,能够更加灵活地适应多目标优化问题,从而更有效地寻找到最优解。
综上所述,尽管MFEA算法在某些优化问题上表现出色,但在处理雷达任务时可能并不是最佳选择。相比之下,MKTC-ES 算法在处理高维度的雷达优化问题时表现更加出色,具有更快的收敛速度和更优异的性能,因此更适合应用于雷达系统的优化设计中。
5 结束语
针对在求解多个自适应雷达任务时,雷达发射器不能满足所有任务需求的问题。本文提出的MKTC-ES 算法将已经学习到的优化策略和信息迁移到新的雷达任务求解中。避免每个任务都需要从头开始学习优化策略,节省了大量的计算资源和时间。基于MKT 方法的通用性,可以更好地适应不同的任务需求和环境条件。MKTC-ES 算法在元知识转移中以更简便的方式得到种群分布信息。并提出指导种群进化方向的“进化路径”在任务间进行了知识共享。为解决雷达波形发射中存在的物理约束,提出适应惩罚函数与CMA-ES算法相结合,将多任务进化算法拓展到了更具有普遍性的带约束条件的问题上。与经典的注水算法相比,本文提出的方法可以同时求解多个任务的同时,求解出的波形具有更高的性能。相较于单独的约束进化算法MKTC-ES算法通过任务间的元知识共享可以更快地寻找到最优发射波形。
[1]崔国龙,余显祥,杨婧,等.认知雷达波形优化设计方法综述[J].雷达学报,2019,8(5):537-557.
[2]余若峰,杨威,付耀文,等.面向不同雷达任务的认知波形优化综述[J].电子学报,2022,50(3):726-752.
[3]徐勇军,曹娜,陈前斌.通信感知一体化波形设计方法综述[J].重庆邮电大学学报(自然科学版),2023,35(6):981-991.
[4]AIAEE-KERAHROODI M, RAEI E, KUMAR S, et al.Cognitive Radar Waveform Design and Prototype for Coexistence with Communications[J].IEEE Sensors Journal,2022, 22(10):9787-9802.
[5]DENG Minglong, CHENG Ziyang, WU Linlong, et al.One-Bit ADCs/DACs Based MIMO Radar: Performance Analysis and Joint Design[J].IEEE Trans on Signal Processing,2022, 70:2609-2624.
[6]CHENG Ziyang, WU Linlong, WANG Bowen, et al.Relative Entropy-Based Constant-Envelope Beamforming for Target Detection in Large-Scale MIMO Radar with Low-Resolution ADCs[J].IEEE Trans on Vehicular Technology,2023, 72(8):10090-10106.
[7]BELL M R.Information Theory and Radar Waveform Design[J].IEEE Trans on Information Theory, 1993, 39(5):1578-1597.
[8]WANG Bin, CHEN Xu, XIN Fengming, et al.MI-Based Robust Waveform Design in Radar and Jammer Games[J].Complexity, 2019(2):1-14.
[9]辛凤鸣,罗晨,张晨雪,等.电子战中基于互信息准则的双鲁棒波形设计[J].电子测量与仪器学报,2023,37(12):84-97.
[10]杨庆培,尚朝轩,董健,等.基于最大边缘分配算法的雷达博弈波形设计[J].电讯技术,2021,61(2):157-163.
[11]YAO Yu, ZHAO Junhui, WU Lenan.Cognitive Radar Waveform Optimization Based on Kalman Filtering for Target Estimation[J].Journal of Applied Remote Sensing, 2018, 12(3):035016.
[12]XIAO Yu, DENG Zhenghong, WU Zhenghong.Information-Theoretic Radar Waveform Design Under the SINR Constraint[J].Entropy, 2020, 22(10):1182-1198.
[13]DE MELO V V, IACCA G.A Modified Covariance Matrix Adaptation Evolution Strategy with Adaptive Penalty Function and Restart for Constrained Optimization[J].Expert Systems with Applications, 2014, 41(16):7077-7094.
[14]赵俊龙,李伟,甘奕夫,等.杂波条件下利用一维卷积神经网络的认知雷达波形设计[J].西安交通大学学报,2021,55(4):69-76.
[15]张嘉翔,张凯翔,梁振楠,等.一种基于深度强化学习的频率捷变雷达智能频点决策方法[J].雷达学报,2024,13(1):227-239.
[16]LI Yanchi, GONG Wenyin, LI Shuijia.Multitasking Optimization via an Adaptive Solver Multitasking Evolutionary Framework[J].Information Sciences, 2023, 630:688-712.
[17]LI Jianyu, ZHAN Zhihui, TAN Kaychen, et al.A Meta-Knowledge Transfer - Based Differential Evolution for Multitask Optimization[J].IEEE Trans on Evolutionary Computation, 2022, 26(4):719-734.