0 引 言
目前,利用遥感技术进行飞行器自主导航定位常用光学图像和SAR(Synthetic Aperture Radar)图像或二者的数据融合,然而,光学图像易受到光照及天气的影响,SAR 图像易受到大气湍流等影响而产生方位向散焦。相较于光学图像,由雷达高度表获得的DDM图像因不受光照条件限制而具有全天时、全天候的工作能力,且不同于依赖侧视长时相干积累形成的SAR 图像,由SARAL(Synthetic Aperture Radar Altimeter)正下视得到的DDM图像相干积累时间短,所需脉冲数少。同时,合成孔径雷达高度表在方位向引入合成孔径思想,通过同时发送多个脉冲并接收多个回波信号,利用多普勒延时技术获得比实孔径雷达更高的分辨率。因此,在起伏地形下获取机载合成孔径雷达高度表机下点照射区域的DDM 成像结果,实现对大型飞行平台可用精度的图像匹配定位,对GPS拒止情况下飞行器自主定位导航具有重要意义。
然而在实际应用中,SARAL 的正下视工作方式使得所成DDM 图像具有近垂直耦合的特点,即由于天线波束具有一定宽度,波束向下照射时,可能会面临与飞行器相距较近的回波信号先被接收,而天底点的信号后被接收的情况,易导致相邻位置的雷达图像差异极小,且由于SARAL 的短时观测特性,易导致所成图像缺少全局特征。同时,由于左右两侧散射点的信息混叠于图像中心,以及散斑噪声的影响,在一定程度上降低了图像的质量。此外,对于同一区域地形来说,当飞行器的飞行状态不同时,所成DDM图像的形态也不同,正确匹配的难度较大。
目前,图像匹配方法可以分为基于图像灰度信息[1]的方法和基于图像特征[2]的方法[3-5]。基于灰度信息方法的核心思想是利用图像的灰度信息来完成图像的匹配,该类方法虽无需分割图像及提取图像特征的特性就可以将预处理所造成的精度损失降到最低[6],但对成像条件、图像形变以及噪声极其敏感,同时具有较高的计算复杂度,从而限制了其应用能力[7]。基于特征方法的核心思想是利用图像中点、线、面等能够表示图像特征的信息来完成图像的匹配[8-9],特征是对局部信息的抽象描述,在保留图像关键信息的同时又大大减少了数据量,很好地弥补了基于灰度方法匹配的缺点,对各种变化的鲁棒性很好[10],计算速度快同时具有较好的匹配精度[11],因此在图像匹配领域被广泛应用。
早期图像匹配方法以特征点检测为主,如加拿大教授Lowe提出的经典尺度不变特征变换方法SIFT[12]等,该方法对旋转、尺度缩放、亮度变化等保持不变性[13-14],但随着系统对实时性、精确性和鲁棒性要求的日益提高,以SIFT 为代表的人工定义的特征算子已无法满足需求[15]。随着人工智能深度学习技术的兴起,使用卷积神经网络的方法进行局部特征点提取的性能已经远超SIFT 特征,如Yi 等提出的LIFT[16]网络,但由于点特征类算法对图像质量要求较高,通常情况下不适用于图像质量较低的DDM图像匹配。针对输入数据的特殊性,近年来将具有双输入数据特点的孪生网络[17]结构搭配对比损失函数协同使用的方法成为图像匹配的主流,但对比损失中负样本是依靠弱先验性均匀随机选取的,在相似度较高的DDM 匹配任务中性能表现较差。
针对上述问题,本文提出了一种基于DDMMPN 的飞行器匹配定位方法,该方法使用浅层卷积神经网络对DDM 图像进行特征提取,同时使用三元组损失、交叉熵损失与中心损失函数以加权的方式协同优化网络参数,充分利用正负样本关注图像的细粒度区别,以提高匹配成功率。此外,由于传统图匹配网络的最终输出为相似度,并不能实现飞行器的坐标定位,故在图匹配神经网络的基础上增加坐标输出模块。最后针对所提网络在不同航迹点下进行模拟仿真实验,地形数据选用湖北十堰市飞行场景,平台模拟为机载平台,雷达频段为Ka 波段,雷达口径为0.3 m,并通过与传统孪生网络搭配对比损失方法及ResNet18、VGG16等深层卷积神经网络进行数据对比,验证了所提网络对SARAL 所成DDM 匹配的有效性、鲁棒性、优越性与高效性。
1 机载SARAL几何与信号模型
1.1 几何模型
机载SARAL 的几何模型如图1 所示。如图1(a)所示,机载SARAL 沿一直线进行飞行运动,在一段较短的飞行距离内对同一地物目标的回波信号进行接收并进行解线性调频及RVP(Residual Video Phase)校正等处理[18]。根据波束区域内不同角度的地物会产生不同多普勒频率的基本原理,利用多普勒波束锐化技术(Doppler Beam Sharpening, DBS)将一个真实天线波束进一步细分为若干个子波束,即所谓的锐化[19],以获得比真实波束更精细的方位向分辨能力。图1(b)表示根据多普勒频率对同心圆形式的脉冲足迹添加等距线和多普勒线进行细分,细分后的脉冲足迹均代表一回波信号[20]。其中,方位向为飞行器的飞行方向,距离向为观测表面垂直于飞行方向的方向。
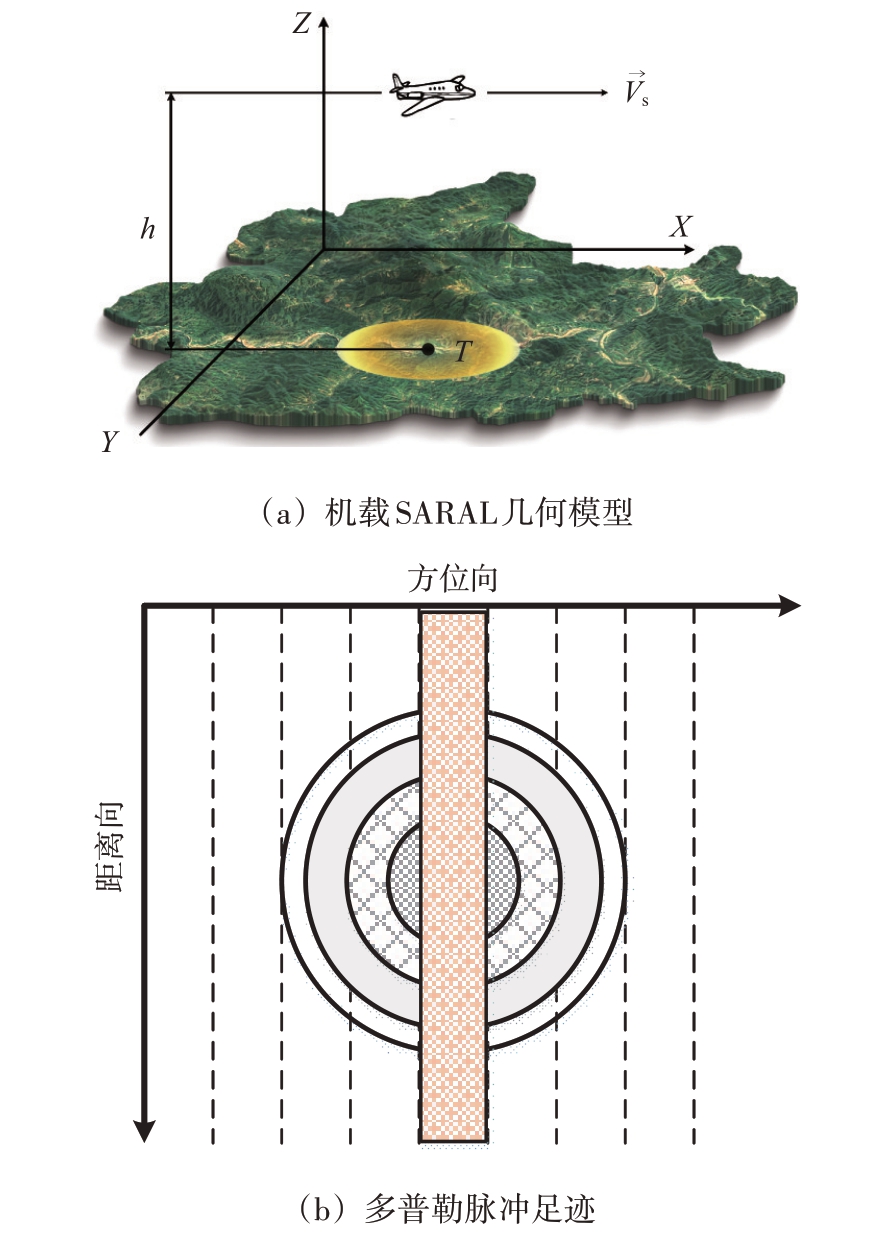
图1 合成孔径雷达高度表工作原理示意图
1.2 信号模型
如图1(a)所示,机载SARAL 以恒定速度Vs 沿高度为h0,方向为X 轴的航迹飞行,地面散射点目标T 的坐标设置为(x0, y0, z0)。当机载SARAL 经过点目标T 正上方时,垂直距离h =| |h0 - z0 ,经时延后接收到的回波信号如下:

式中,t和ts分别为距离向快时间和方位向慢时间,A0为散射系数,![]() 为SARAL与地面目标T 之间的斜距,href 为SARAL 到目标表面高度的粗略估计,fc 为载波频率,Kr 为调制频率,c 为光速。接收到的回波信号经解线性调频后可得式(2)。
为SARAL与地面目标T 之间的斜距,href 为SARAL 到目标表面高度的粗略估计,fc 为载波频率,Kr 为调制频率,c 为光速。接收到的回波信号经解线性调频后可得式(2)。
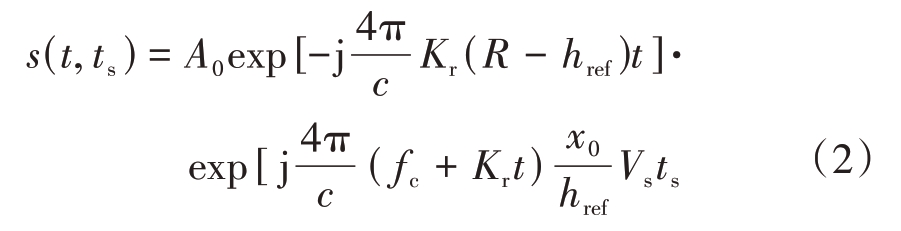
沿航向对式(2)通过FFT 进行DBS 处理,即可得到DDM 图像X 的表示式(3)。其中fd(m)为SARAL产生的第m个多普勒频率。
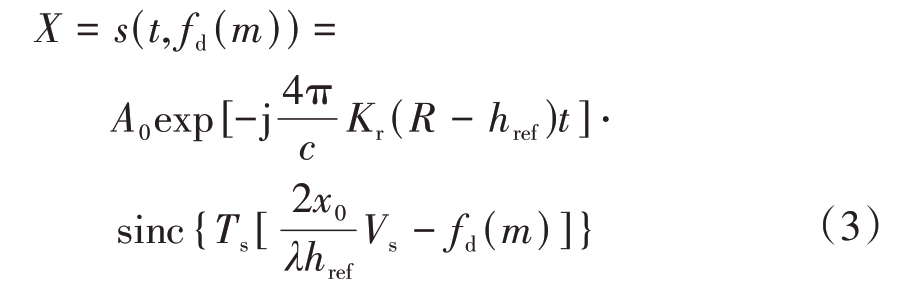
回波经上述处理后获得DDM 图像X,其示意图如图2 所示。其中,横坐标代表距离门,纵坐标代表多普勒频率。
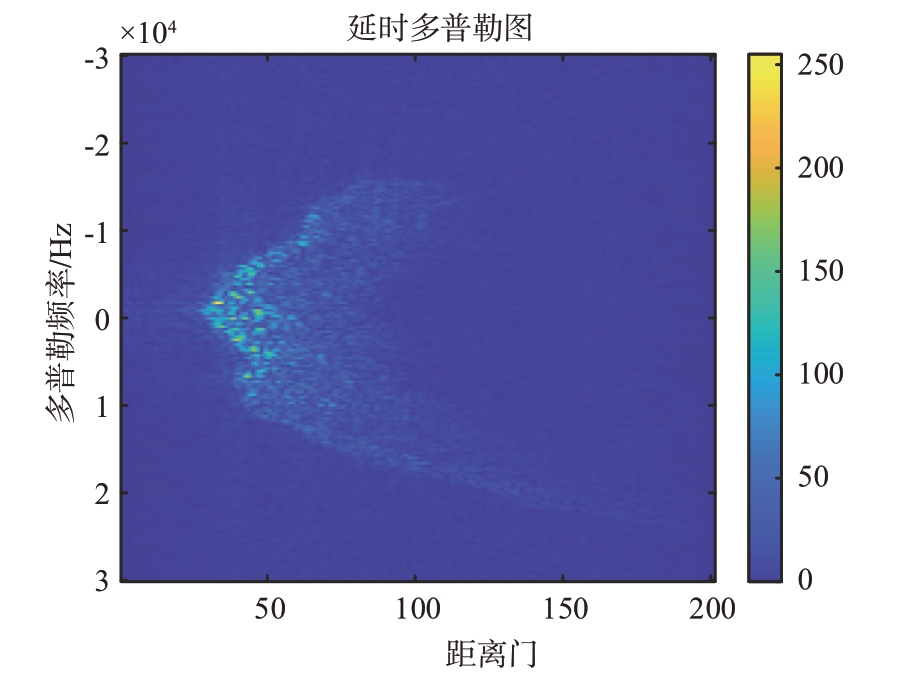
图2 DDM示意图
2 延时多普勒匹配定位网络
基于延时多普勒图像的匹配定位方法流程图如图3 所示。网络输入为实时图像和预存的匹配基准图像,将输入图像分别输入到经训练的卷积神经网络进行特征提取,以获得其特征嵌入表征向量,同时利用ℓ1 正则化对网络进行模型约束,以缓解模型过拟合。再将实时图像的特征嵌入表征向量与预存的匹配基准图像的特征嵌入表征向量集合进行相似度的遍历计算,对不同地形数据重复匹配步骤可得到相似度列表,将相似度列表降序排列,取相似度最高处坐标或相似度前三处坐标平均值作为飞行器当前的定位坐标。
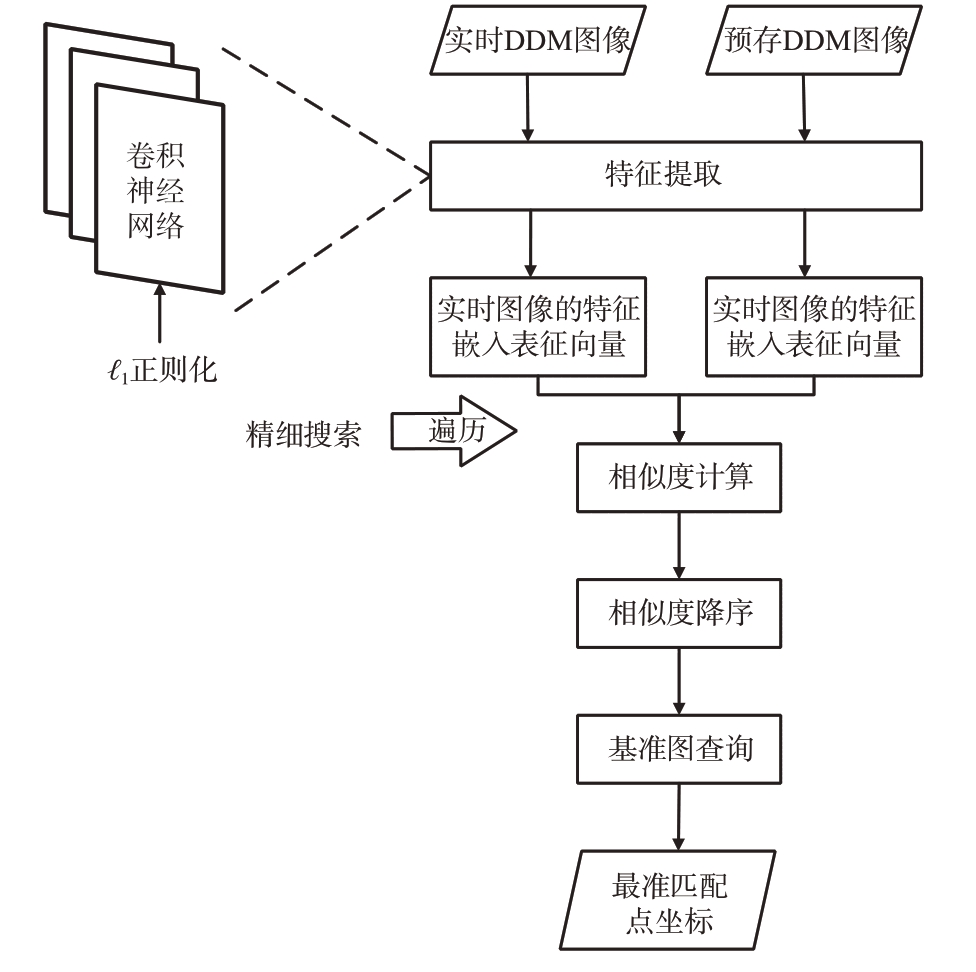
图3 基于延时多普勒图像的匹配定位方法流程图
2.1 基于卷积神经网络的特征提取网络
本文的特征提取框架采用计算机视觉和图像处理问题中常用的卷积神经网络,区别于Res-Net18、VGG16 等经典深层卷积网络,本实验搭建了一个7层卷积的浅层卷积网络,用更少的参数和训练时间可达到与重量级神经网络相当甚至更高的定位精度和匹配成功率。
所用卷积神经网络的具体网络参数如图4 所示。网络的输入为201×201大小的灰度图。其中,“3 × 3 conv, 32”表示卷积核大小为3×3,卷积核个数为32 的卷积层,不加“/2”的层默认卷积步长为1,否则为2。除最后一层外其余各层之后的激活函数均为ReLU 函数。输入图像共经过7 层卷积,后经最大池化和展开后得到输出的特征嵌入表征向量。
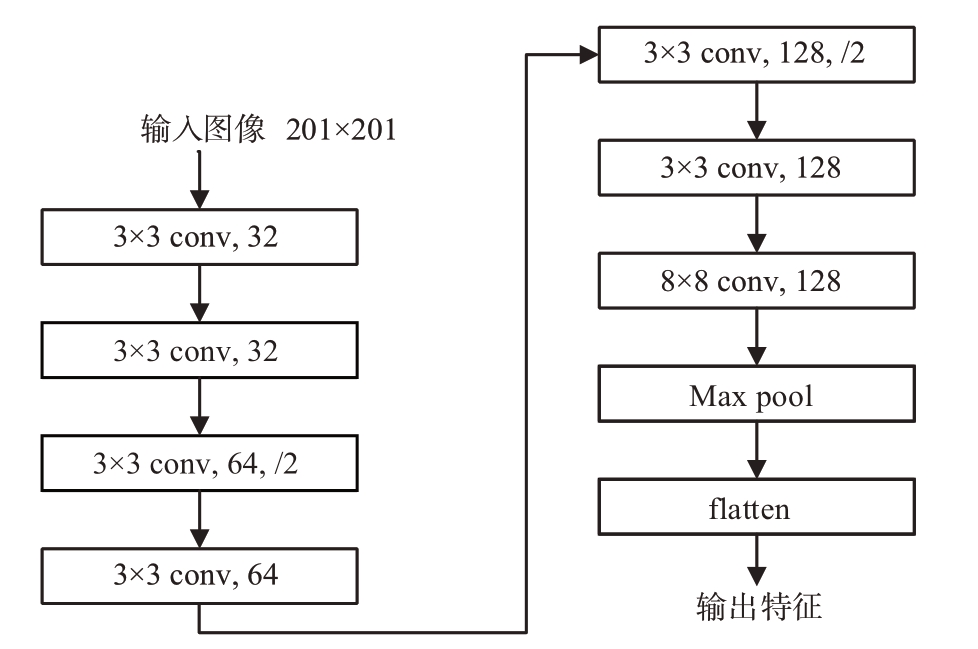
图4 特征提取网络
2.2 损失函数
通常,图像匹配任务的损失函数构建在样本对或者样本三元组之上,因而样本空间的量级非常大。基于样本对的损失函数称为对比损失函数[17],基于样本三元组的损失函数称为三元组损失函数[21],三元组损失函数因考虑了正负样本与锚点之间的距离关系而在细节区分上有明显的优势,在相邻地形极为相似的DDM 图像上匹配成功率明显优于对比损失函数,故在实验中采用三元组损失函数。但模型在训练过程中很难穷举学习所有的样本三元组,且大多数样本三元组在模型训练的后期信息量很小,使得其梯度值几乎为0。若不采取有针对性的样本选取策略,网络的收敛速度会很慢,且易陷入局部最优,因此,常配合困难样本挖掘的学习策略一起使用,且大多数情况下会与分类损失结合使用。本实验共采用了3 种损失函数,分别为困难样本三元组损失函数、中心损失函数和交叉熵损失函数,3 种损失函数协同作用优化网络参数。网络损失函数可表示为
式中,Ltriplet 为三元组损失函数,Lcenter 为中心损失函数,β 为中心损失权重,实验中设置β = 0.001,LEN为交叉熵损失函数。
三元组损失函数的基本思想如图5所示,设定一个样本三元组分别为基准样本(Anchor)、正样本(Positive)和负样本(Negative),其中,基准样本和正样本为同类的不同样本,基准样本与负样本为异类样本。三元组损失函数试图学习到一个特征空间,使得在该空间中相同类别的基准样本与正样本的距离尽可能接近,不同类别的基准样本与负样本的距离尽可能拉远[21]。
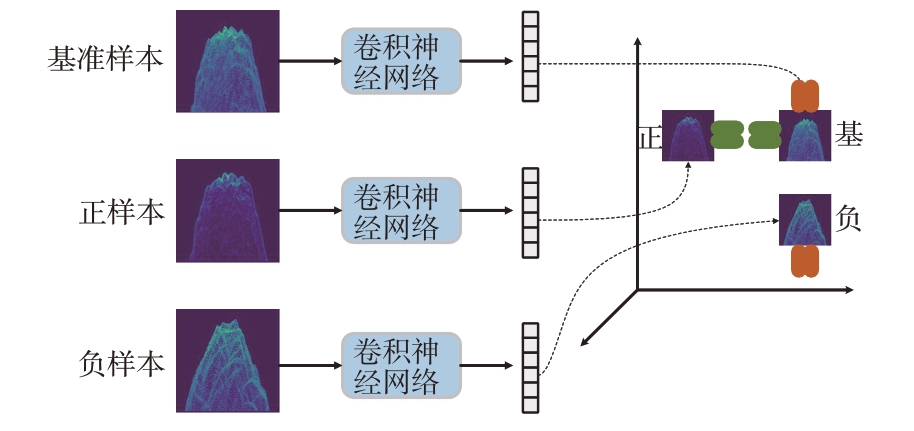
图5 三元组损失函数基本原理
根据上述原理,假设![]() 作为一组数据输入到卷积神经网络中,并得到对应的特征映射
作为一组数据输入到卷积神经网络中,并得到对应的特征映射![]() ,其中下缀i表示第i个批次,f(·)表示网络等效的函数,上缀a、p、n表示对应的三元组样本,则三元组损失函数的思想用欧氏距离形式化可以表示为
,其中下缀i表示第i个批次,f(·)表示网络等效的函数,上缀a、p、n表示对应的三元组样本,则三元组损失函数的思想用欧氏距离形式化可以表示为
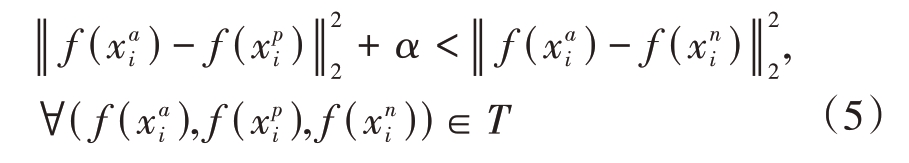
式中α 为间隔参数margin,T 是训练集中所有可能三元组的集合,基数为N。此时,三元组损失函数可以表示为

其中下标“+”表示:当中括号中的式子的值大于零时,即不满足不等式(5)时,此时损失大于零,网络通过反向传播更新参数;当中括号中的式子的值小于零时,即满足不等式(5)时,表示样本已满足训练要求,此时不产生梯度,网络参数不更新。而我们的目标就转变为训练网络模型使得式(6)的损失函数不断变小。
然而,三元组损失函数只考虑了样本间的相对距离,而没有考虑样本间的绝对距离。为了在保持类间特性可分离的同时最小化类内间距,引入中心损失函数,中心损失为每个类别提供了相应的类别中心,即一个与特征嵌入表征向量具有相同维度的向量[22]。该损失函数通过学习每个类别的中心,使得类内的距离变得更加紧凑,弥补了三元组损失函数的缺点,表达式如式(7)所示。
式中,xi 为全连接层前的特征嵌入表征向量,yi 为一个批量中的第i 个图像的标签,cyi ∈Rd 为特征的第yi个类中心,B为批大小。
同时,参考行人重识别任务中常用的身份损失(ID Loss),实验采用交叉熵损失函数对网络进行协同约束,其中每一个类别为一个地形坐标值。
标准交叉熵损失函数原理如下。对于每个样本x 计算归属每个标签i ∈{ }1, 2,…, N 的预测概率为

式中,zi 为神经网络的输出,称为逻辑分数或未归一化的对数概率。设该样本标准化的真实标签分布为qi,那么有∑iqi = 1。简洁起见,忽略p 和q 对样本x的依赖关系,设y为真值标签,定义交叉熵损失函数如下:

2.3 样本选取策略
采用三元组损失函数的一个问题是训练集中生成的所有可能三元组中,可能生成许多容易满足约束式(5)的三元组。这些三元组称为简单样本三元组,对训练并没有实际帮助,并且会导致更慢的收敛速度和更差的泛化性能,因为它们仍然会通过网络。所以使用三元组损失函数的一个关键是尽可能选择难训练的三元组样本,即尽可能满足式(10),它们是活跃的,因此可以帮助改进模型,称为困难样本三元组。
式(10)表示负样本与基准样本间的距离小于正样本与基准样本间的距离,这是网络最难学习的样本组。但此时的损失值会出现较大的震荡,易出现网络难收敛和模型崩溃的问题。
故本实验采用半难样本三元组。半难样本三元组满足式(11),即负样本比正样本距离基准样本更远,但是距离差没有达到设定间隔,如图6所示,此时网络通过恰当的学习可以不断降低损失值,模型既可以学习到样本之间的差异,又较容易收敛。
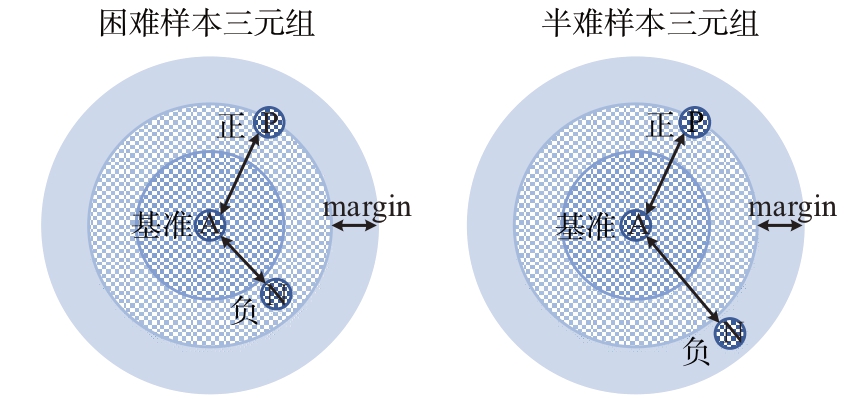
图6 困难样本三元组与半难样本三元组对比
从一个批量的B 个特征向量中挖掘半难三元组的方法如下。假设索引i, j, k ∈[1, B],其中i 和j(i ≠j)具有相同的标签,k 具有不同标签,此时(i, j, k)被称为是一个有效三元组。假设一个批数据,由P 个坐标点、每个坐标点下K 张增强DDM 图像构成,即批大小B = P × K。此时可能产生PK(K - 1)(PK - K)个合规的三元组,其中基准样本有PK 个,正样本有(K - 1)个,负样本有(PK -K)个。对于每个基准样本,挑选一个最难正样本和最难负样本,即最小相似度正样本与最大相似度负样本,这个过程共产生了PK 个三元组,此时三元组损失可表示为
总的来说,延时多普勒匹配定位网络的训练通用流程共包含3 个部分,即为特征提取网络、样本选取策略及损失函数,如图7所示。
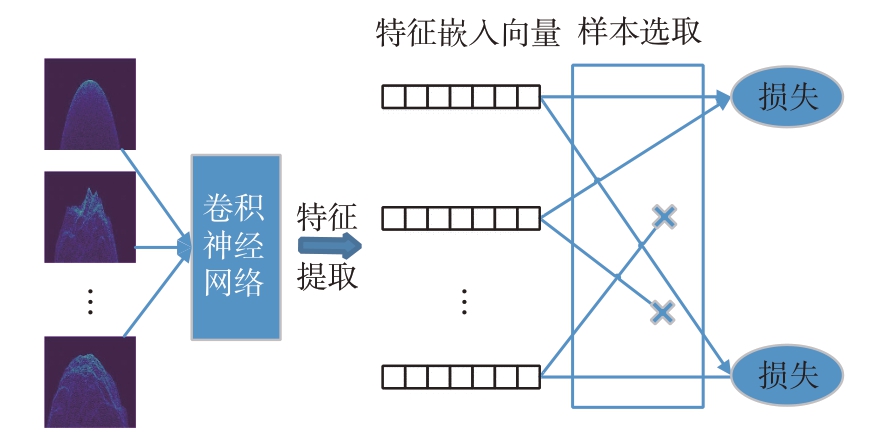
图7 DDM-MPN训练通用流程图
3 实验验证
基于延时多普勒图像的匹配定位算法由训练过程与测试过程构成,其训练过程流程图如图8所示。训练过程包括5 个主要部分:首先将训练集设置为不同坐标点下的基准仿真DDM 图像数据集,并对其进行数据增强;训练时从上述数据集中的不同坐标位置随机抽取批量大小的图像,并输入到卷积神经网络中进行特征提取;根据特征嵌入表征向量的距离度量选取三元组样本;锚样本、与锚样本标签一致的正样本对和与锚样本标签不一致的负样本对的相应特征用于三元组损失函数及中心损失函数的计算,再通过分类器后得到分类结果,用于交叉熵损失函数的计算;再经反向传播对网络参数进行优化,最后得到较好的网络模型。
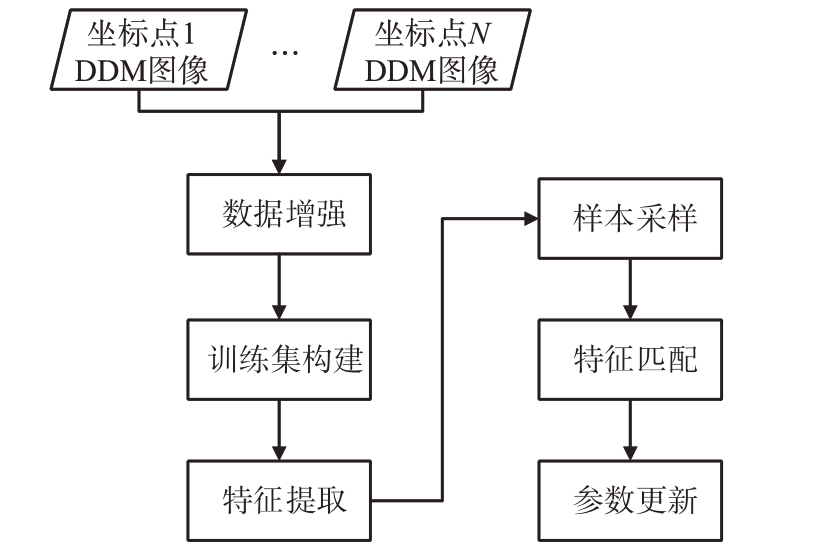
图8 DDM-MPN训练过程
其测试过程流程图如图9 所示,包括5 个主要部分:首先将测试集设置为与训练集数据隔离的实测DDM 图像数据集和预存的网格点仿真DDM图像数据集,并且对数据集中图像进行预处理;将测试集中所有的实测DDM 图像及预存仿真DDM图像输入训练后的网络中进行特征提取得到相应的特征嵌入表征向量;之后,利用某地形下的实测图与预存在飞行器基准图库中的所有图像进行遍历匹配;接着将网络输出转换为余弦相似度,得到匹配相似度列表;最后将相似度列表降序排列,取出相似度最高值或相似度前三对应的基准图索引,该基准图的坐标或3个基准图的坐标平均即为网络预测的当前飞行器的实时坐标。
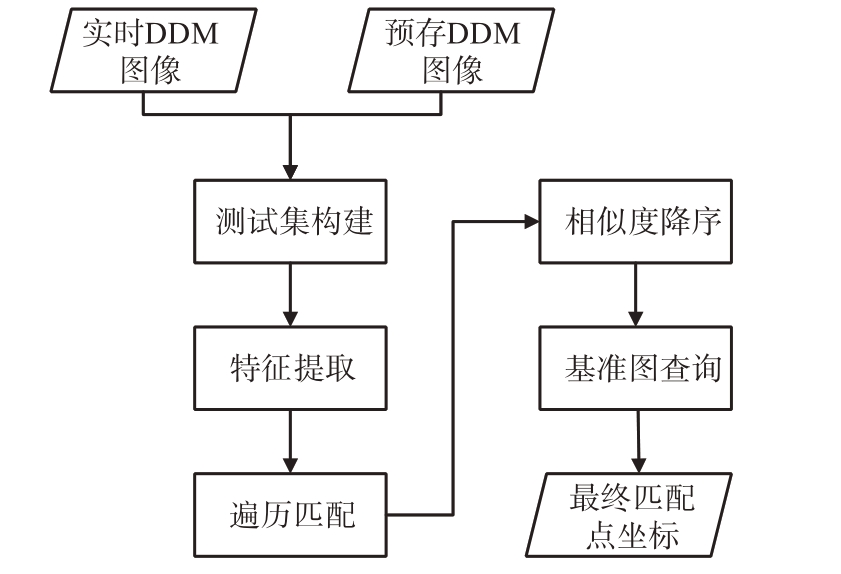
图9 DDM-MPN测试过程
基于以上的匹配算法进行模型训练,测试匹配的精度和成功率,并与传统的基于对比损失的孪生网络匹配方法进行比较。实验采用的深度学习框架为Pytorch,评价指标为定位精度和匹配成功率。定位精度采用均方根误差(RMSE)衡量,公式如下:
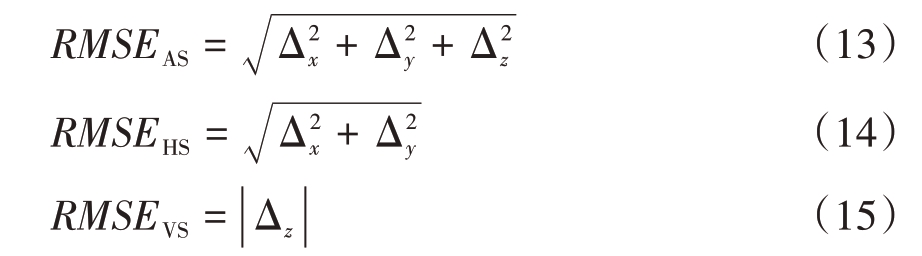
式中,RMSEAS、RMSEHS 和RMSEVS 分别表示三维总体误差、水平面内误差和垂直航向误差,单位为m,Δx、Δy 和Δz 分别表示x 方向、y 方向和z 方向上的坐标误差。
由于垂直航向上高度几乎不变,默认平飞,故本实验将单次匹配中RMSEHS ≤50 m的匹配结果视为匹配成功,自定义匹配成功率的计算公式如下:
式中,N为匹配成功的次数,M为总匹配次数。
3.1 数据集制备
该方法适用于复杂地形场景,故实验中选用湖北十堰市飞行场景,如图10所示,横向延伸55 km,纵向延伸37 km。数据集的制备方式为在地图中随机选取5 000 个坐标点,并在每个坐标点下生成对应的DDM 图像,均为灰度图像,图像尺寸为201×201。前4 000 个坐标点作为训练集坐标库,从中抽取2 000个坐标点作为训练数据集,后1 000个坐标点作为验证集坐标库,从中抽取200个坐标点作为验证数据集。与传统中心裁剪、翻转、随机擦除等数据增强方式不同,本实验对DDM 图像以直方图均衡、加乘性噪声、加加性噪声、边缘增强等方法进行数据增强。通过正负样本对的组合,生成24 000张训练图像和2 400张验证图像。
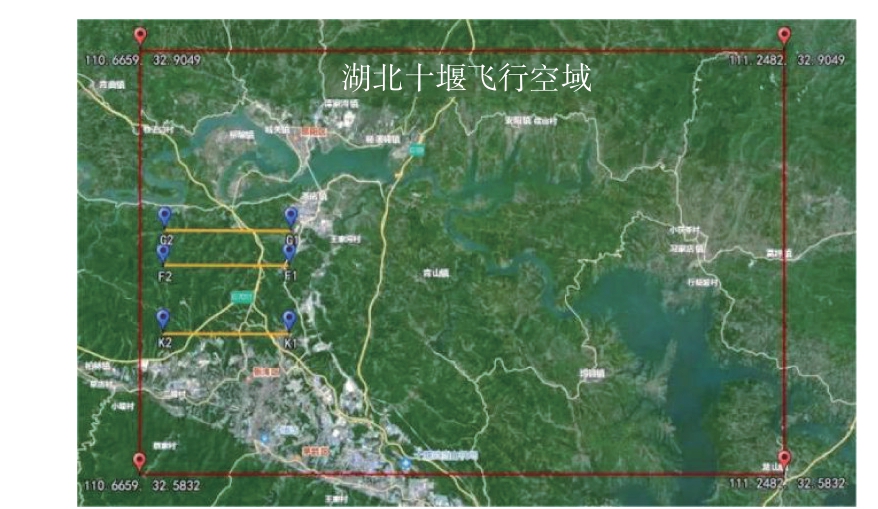
图10 湖北十堰市飞行场景
测试集由与训练集数据隔离的预设航迹上的实测DDM图像数据集构成,如图中航迹F1-F2、G1-G2、K1-K2 等。网格点的划分采用离线划分的方式,如图11所示,即假设飞行器出发和到达的时间地点是确定的,那么大致的飞行方向以及飞行速度可以假设处于一个较小且可以忽略的置信区间,离线在已有轨迹的9 km 范围内,建立100 个坐标点当作测试基准点,以100 m 为间隔上下左右划分网格坐标点,并依照预定的速度状态生成参考基准图像。
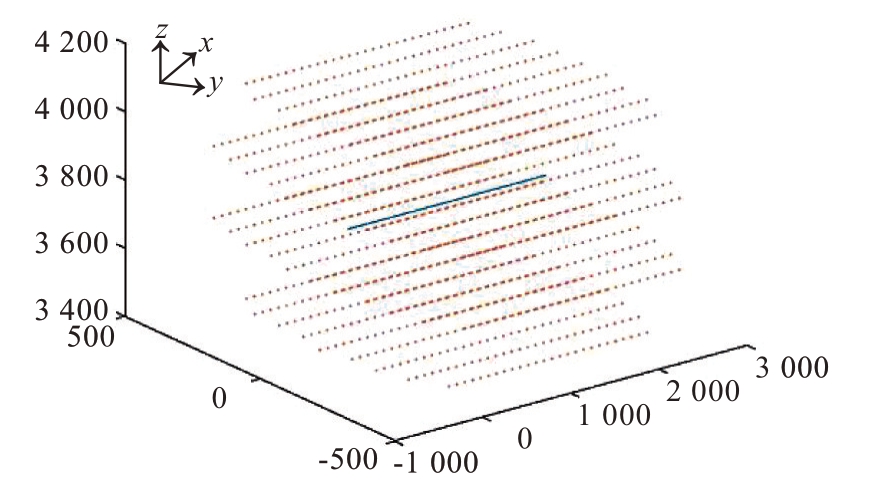
图11 离线网格划分示意图
3.2 模型训练
训练参数设置如下:批大小为32,训练总轮次为120,模型梯度优化算法使用Adam,学习率为0.000 35,权重衰减为0.000 1,中心点的更新独立于模型更新,梯度优化算法使用随机梯度下降,学习率为0.5。
因三元组损失函数增加了模型的复杂度,同时引入ℓ1 范数正则化对网络进行模型约束以缓解模型过拟合现象。该方法通过向损失函数中添加ℓ1 范数,从而产生稀疏权值矩阵,即产生一个稀疏模型,使得学习得到的特征满足稀疏化,便于进行特征的选择,故ℓ1 正则化可以看作损失函数的惩罚项。ℓ1 正则化是指权重向量w 中各个元素的绝对值之和,通常表示为‖ w ‖1。加入ℓ1 正则化的损失函数可表示为
式中,L(w)为模型原始损失函数,λ为正则化系数,用于控制正则化的强度,实验中设置λ=0.000 3。最终模型在训练过程中的损失函数曲线如图12所示,可以看出,在第40个轮次左右神经网络对训练集的损失均已达到较稳定数值。
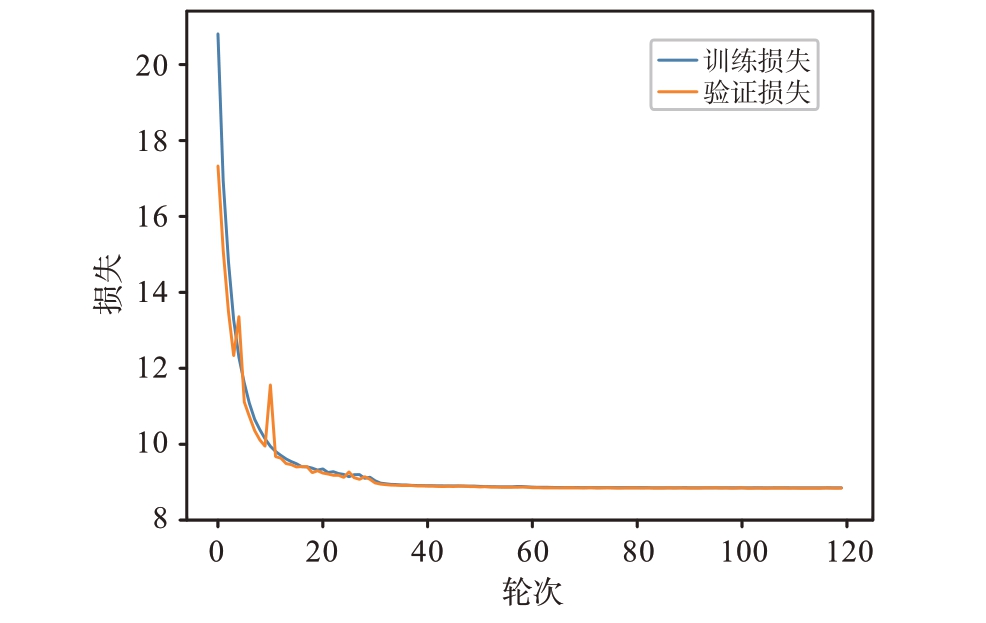
图12 损失曲线
3.3 性能分析
为了验证模型的有效性,选取湖北十堰市飞行场景中G1-G2 航段对模型进行测试。首先,将本实验所用基于3 种损失函数的DDM-MPN 网络与图像匹配任务常用基于对比损失的双输入孪生网络进行对比测试,测试结果如表1 所示。3 个衡量性能的指标分别为水平面平均定位误差、垂直航向平均定位误差及三维总体平均定位误差。可以看出,传统基于对比损失的孪生网络所得定位误差较大,无法满足水平面误差小于50 m 的要求,而本实验所提匹配算法有更高的定位精度和更稳定的匹配性能。
表1 不同方法对比

网络Siamese Network DDM-MPN单点匹配定位多点加权匹配定位RMSEHS/m 2 639.544 42.920 RMSEVS/m 178.085 65.756 RMSEAS/m 2 658.816 90.444 RMSEHS/m 2 347.284 35.665 RMSEVS/m 88.142 57.764 RMSEAS/m 2 355.248 72.014
为了验证模型在不同飞行场景下的鲁棒性,在湖北十堰市飞行场景中选取F1-F2、G1-G2及K1-K2 航段对模型进行测试,测试结果如表2 所示。从表中可以看出,不同航迹下利用多点加权匹配定位所得定位误差基本稳定在100 m 及以下,匹配成功率均在80%及以上,即训练完成的DDM-MPN网络具备一定的飞行场景泛化能力。
表2 不同飞行场景对比

航段F1-F2 G1-G2 K1-K2单点匹配定位多点加权匹配定位RMSEHS/m 38.769 42.920 34.092 RMSEVS/m 95.563 65.756 70.311 RMSEAS/m 114.949 90.444 86.502 ACC/%77 73 79 RMSEHS/m 33.271 35.665 44.990 RMSEVS/m 93.106 57.764 70.876 RMSEAS/m 103.573 72.014 94.360 ACC/%87 80 85
本实验共试验了3种网络骨干模型,其中包括计算机视觉任务常用的网络ResNet18、VGG16 及本实验所用网络DDM-MPN。3个网络模型的定位表现如表3 所示。从表中可以看出,VGG16 和DDM-MPN 的定位表现较为良好,其中,DDM-MPN的单点匹配和多点加权匹配的水平面平均定位误差、垂直航向平均定位误差及三维总体平均定位误差均较低。
表3 不同模型定位误差对比

网络名称ResNet18 VGG16 DDM-MPN单点匹配定位多点加权匹配定位RMSEHS/m 52.872 37.931 42.920 RMSEVS/m 73.944 112.550 65.756 RMSEAS/m 103.958 131.184 90.444 ACC/%61 78 73 RMSEHS/m 97.671 37.396 35.665 RMSEVS/m 70.259 91.879 57.764 RMSEAS/m 139.572 104.216 72.014 ACC/%64 86 80
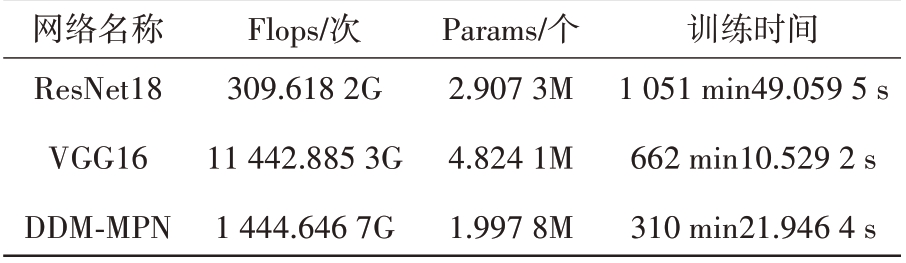
3种网络的模型复杂度对比如表4所示,其中,Flops表征浮点运算数,可以理解为计算量,用来衡量模型的复杂度,Params 表征模型参数量。可以看出,本文所用网络DDM-MPN 的模型复杂度中等,模型参数量最少,且训练所用时间最短。
表4 模型复杂度和参数量对比
网络名称ResNet18 VGG16 DDM-MPN Flops/次309.618 2G 11 442.885 3G 1 444.646 7G Params/个2.907 3M 4.824 1M 1.997 8M训练时间1 051 min49.059 5 s 662 min10.529 2 s 310 min21.946 4 s
DDM-MPN 匹配定位误差可视化如图13所示。当取相似度最高的网格点坐标作为最终定位坐标时,测试结果如图13(a)所示,称为单点匹配。当取相似度前三的网格点坐标平均作为最终定位坐标时,测试结果如图13(b)所示,称为多点加权匹配。其中,虚线代表水平面误差,即最终定位坐标的x 轴、y 轴坐标与基准点x 轴、y 轴坐标之间的欧式距离,点线代表垂直航向误差,即最终定位坐标的z 轴与基准点的z 轴坐标的距离绝对值,实线代表三维总体定位误差,最终定位坐标与基准点的三维坐标之间的欧氏距离。
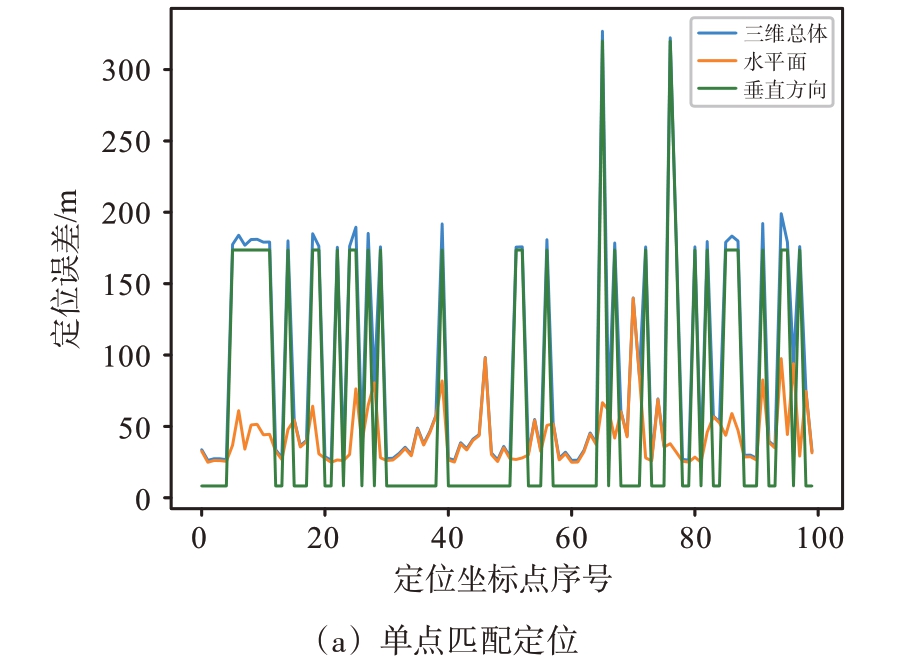
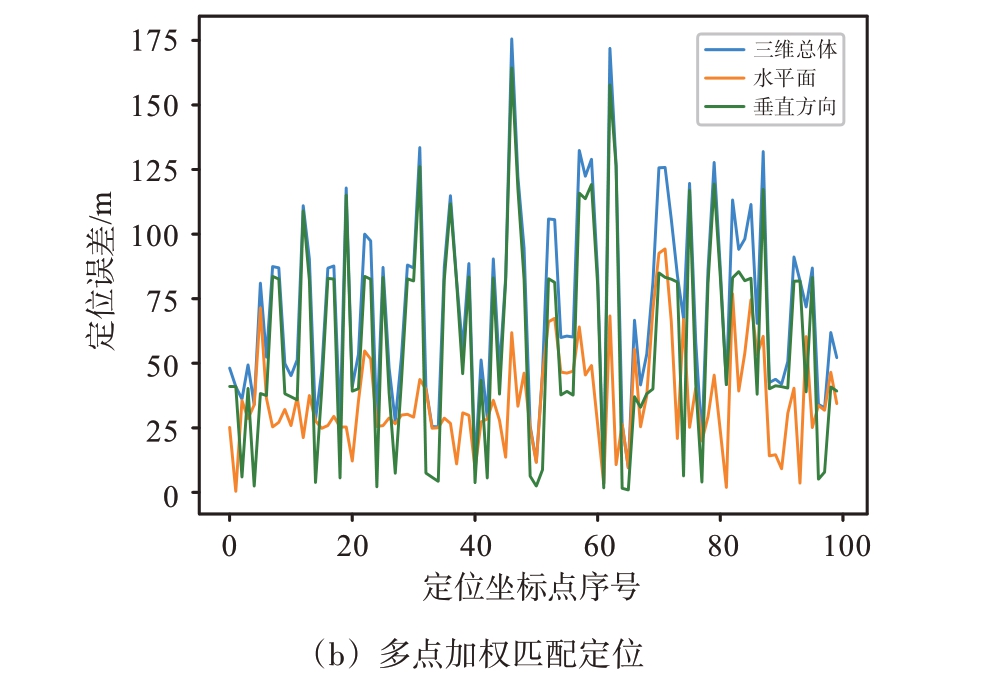
图13 DDM-MPN匹配定位误差可视化
由图中可以看出,基于多点加权匹配的定位结果明显好于基于单点匹配的定位结果,且水平面平均定位误差在30 m 左右,垂直航向平均定位误差在50 m 左右,总体平均定位误差在70 m 左右,对于常见的大型飞行平台,此定位精度在GPS拒止情况下的可用性较高。
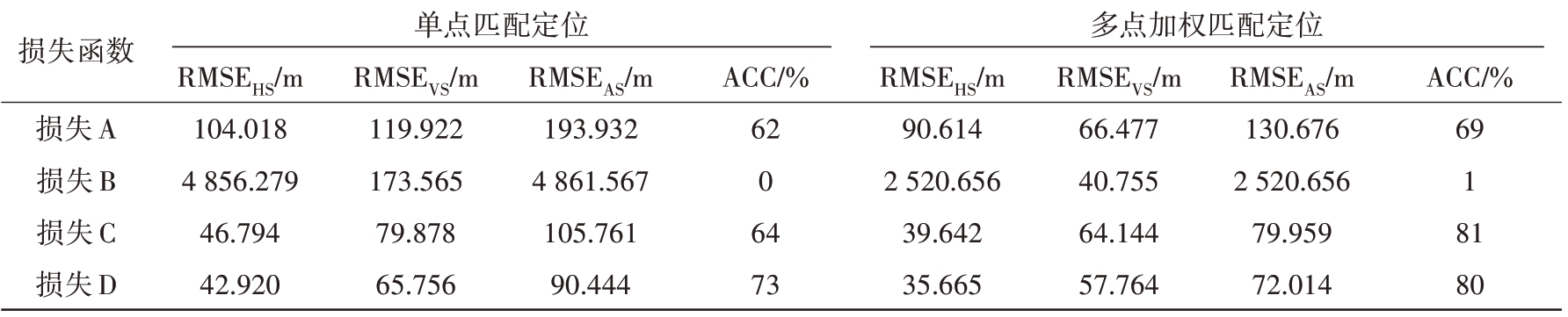
同时,本实验共试验了4 种损失函数,其中包括三元组损失与交叉熵损失(记为损失A)、中心损失与交叉熵损失(记为损失B)、三元组损失与中心损失(记为损失C)、三元组损失中心损失与交叉熵损失三者协同作用(记为损失D)。分别应用这4种损失函数时,模型的定位性能对比如表5 所示。可以看出,采用三元组损失中心损失和交叉熵损失协同优化的方式时,单点匹配定位及多点加权匹配定位的定位误差均最小,且匹配成功率均较高。
表5 不同损失函数定位误差对比
损失函数损失A损失B损失C损失D单点匹配定位多点加权匹配定位RMSEHS/m 104.018 4 856.279 46.794 42.920 RMSEVS/m 119.922 173.565 79.878 65.756 RMSEAS/m 193.932 4 861.567 105.761 90.444 ACC/%62 0 64 73 RMSEHS/m 90.614 2 520.656 39.642 35.665 RMSEVS/m 66.477 40.755 64.144 57.764 RMSEAS/m 130.676 2 520.656 79.959 72.014 ACC/%69 1 81 80
最后,实验对设定阈值margin 的选取进行了对比测试,测试性能如表6 所示。实验表明,选取margin=0.8 时,模型的定位精度可以保持在较高水平,且定位误差可以保持在较低范围内。
表6 不同阈值选取的对比

margin 0.2 0.5 0.8 1.0单点匹配定位多点加权匹配定位mean_HS/m 47.496 44.807 42.920 44.408 mean_VS/m 94.753 95.653 65.756 97.494 mean_AS/m 118.506 118.547 90.444 119.569匹配成功率/%68 66 73 69 mean_HS/m 49.634 38.599 35.665 42.898 mean_VS/m 53.526 57.995 57.764 51.713 mean_AS/m 82.803 74.337 72.014 74.103匹配成功率/%79 79 80 83
4 结束语
本文针对相邻地形DDM 相似度高,利用神经网络对其进行匹配时成功率低的问题,搭建了适用于雷达高度表延时多普勒的匹配定位网络DDMMPN,该网络选取三元组损失、中心损失和交叉熵损失作为目标损失函数,通过对实时DDM 图像和基准DDM 图像进行相似度度量,最终实现了对飞行器的实时坐标定位。实验结果表明,该网络的定位精度和匹配成功率相较传统基于对比损失的孪生网络有较为明显的提升,且训练时间相较深层卷积神经网络较短。
[1]牟金明.异源图像的深度匹配方法研究[D].西安:西安电子科技大学,2022.
[2]王茂琴.基于图像匹配的无人机定位技术[D].西安:西北大学,2022.
[3]MA Jiayi, JIANG Xingyu, FAN Aoxiang, et al.Image Matching from Handcrafted to Deep Features: A Survey[J].International Journal of Computer Vision,2020,129(1):23-29.
[4]徐梦莹,刘文波,郑祥爱,等.基于深度学习的图像特征匹配方法[J].传感器与微系统,2022,41(7):61-64.
[5]刘海桥,刘萌,龚子超,等.基于深度学习的图像匹配方法综述[J].航空学报,2024,45(3):82-95.
[6]贺迅,方敏,郭龙飞,等.基于深度学习的图像匹配方法:中国,CN113111937A[P].2021-07-13.
[7]胡玉珍.基于深度学习的航拍图像匹配方法研究[D].吉林:吉林大学,2023.
[8]刘瑞.基于深度学习的飞行器图像自主导航算法研究[D].南京:南京航空航天大学,2023.
[9]杨济瑞,张晓燕,罗攀.基于图像匹配的特征点检测方法综述[J].电子测试,2021(6):53-54.
[10]廖明哲.基于深度学习的遥感图像匹配方法研究[D].武汉:武汉科技大学,2021.
[11]张源峰.基于图像特征与灰度值的快速匹配算法研究[D].兰州:兰州理工大学,2018.
[12]LOWE D G.Distinctive Image Features from Scale-Invariant Keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.
[13]眭海刚,刘畅,干哲,等.多模态遥感图像匹配方法综述[J].测绘学报,2022,51(9):1848-1861.
[14]于秋则,周珊,雷震,等.基于非线性SIFT 框架SAR 图像匹配[J].雷达科学与技术,2019,17(3):237-245.
[15]贾迪,朱宁丹,杨宁华,等.图像匹配方法研究综述[J].中国图象图形学报,2019,24(5):677-699.
[16]YI K M, TRULLS E, LEPETIT V, et al.LIFT: Learned Invariant Feature Transform[C]// European Conference on Computer Vision, Amsterdam, Netherlands:[s.n.],2016:457-483.
[17]CHEN Xinlei, HE Kaiming.Exploring Simple Siamese Representation Learning[C]//2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA:IEEE, 2021:15750-15758.
[18]杨双宝,翟振和,许可,等.合成孔径雷达高度计数据处理方法[J].遥感技术与应用,2017,32(6):1083-1092.
[19]刘少强,姜军.现代机载火控雷达功能模式[J].移动信息,2015(2):24.
[20]杨磊,周弘昊,黄博,等.机载合成孔径雷达高度计高程参数贝叶斯估计[J].电子与信息学报,2023,45(4):1254-1264.
[21]SCHROFF F, KALENICHENKO D, PHILBIN J.Face-Net: A Unified Embedding for Face Recognition and Clustering[C]//2015 IEEE Conference on Computer Vision and Pattern Recognition,Boston,MA,USA:IEEE,2015:815-823.
[22]WEN Yandong, ZHANG Kaipeng, LI Zhifeng, et al.A Discriminative Feature Learning Approach for Deep Face Recognition[J].European Conference on Computer Vision, Amsterdam, Netherlands:[s.n.], 2016:499-515.