0 引 言
模糊函数（Ambiguity Function，AF）是评估雷达系统目标探测性能的重要工具，反映了波形在时延与多普勒频率维度的相关特性。通过抑制AF特定时延-多普勒区域的旁瓣，可有效提升雷达系统对具有特定距离和速度的目标的探测能力。此外，为使雷达系统非线性功率放大器的工作效率最大化，需要对波形施加恒模约束（Constant Modulus Constraint，CMC）。因此，基于AF 赋型的恒模波形设计引起了广泛关注［1-6］。
目前，解决该问题的方法可分为两类：第一类方法通过松弛该问题进行求解，这类方法引入的松弛误差会导致波形的性能下降；第二类方法直接对该问题求解，但该类方法的超参数选取较为困难，并且运算量较大。
在第一类方法中，文献［7］提出了一种加速迭代序列优化（Accelerated Iterative Sequential Optimization，AISO）方法，该方法通过将原四次问题松弛为一个二次问题降低了求解难度，但是该方法会产生较大的松弛误差。为了解决该问题，文献［8］通过构造原问题的替代函数提出了一种MM（Majorization-Minimization）方法，但是找到契合原问题的替代函数较为困难；为了解决这一问题，文献［9］提出了一种坐标下降法（Coordinate Descent，CD），该方法将原问题分解为多个近似的一维的子问题，避免了构造替代函数，但是该算法的计算复杂度会随着信号长度的增长急剧上升。
在第二类方法中，文献［10］提出了一种分数交替方向惩罚（Fractional-Alternating Direction Penalty，FADPM）方法，该方法通过构建等效的惩罚项避免了对原问题的松弛，但该方法对惩罚参数的选取十分敏感。为了解决该问题，文献［11］提出了一种四阶黎曼信赖域（Quartic Riemannian Trust Region，QRTR）方法，该方法通过构建流形空间直接求解原问题，避免了惩罚参数的选取，但该方法需要计算Hessian 矩阵，因此计算复杂度较高。为了降低计算复杂度，文献［12］提出了一种四阶梯度下降（Quartic Gradient Descent，QGD）方法，该方法仅需要推导一阶黎曼梯度，避免了计算Hessian矩阵，但该方法对步长因子的选取十分敏感。
我们注意到该问题具有明显的非线性特征，而深度学习（Deep Learning，DL）网络具有强大求解非线性问题的能力，并且网络参数可以自适应地更新迭代。因此，我们提出了一种基于深度学习残差网络（Residual Network，ResNet）的AF 赋型方法。首先，我们将该问题转化为一个无约束的相位优化问题。然后，将该问题的非凸目标函数构造为网络的损失函数。最后，ResNet 直接优化波形的相位。
本文的主要贡献如下：
1） 现有的AF 赋型方法面临着松弛误差过大与超参数选取困难的问题，与现有方法不同，我们提出了一种基于深度学习残差网络的AF 赋型方法，该方法无需松弛而且不需要复杂的参数选取，可直接对该复数四次问题进行求解；
2） 与现有方法相比，所提方法的信干比（Signal-to-Interference Ratio,SIR）比文献［9］和文献［12］中的方法分别提高了70.47 dB 和26.86 dB，同时具有更好的目标探测性能。
1 问题模型
考虑一个单输入单输出（Single-Input Single-Output，SISO）的雷达系统，发射的恒模波形为
式中，j为虚数单位，N 为s的长度，y(n) ∈(0,2π]是s 的第n 个相位，(·)T 表示向量的转置。s 的模糊函数可表示为
式中，‖ · ‖2 表示向量的二范数，|· |表示绝对值，(· )H表示向量的共轭转置，Jr为移位矩阵，表示为
yv = s⊙p(v)，⊙表示向量的点乘，其中，p(v) =[1,ej2πv,…,ej2π(N - 1)v ]T，v 为归一化的多普勒频率，对v离散化后可表示为
, h = 0,…,Nv - 1，Nv是离散化的多普勒频点的数量。
根据式（2），s 的加权积分旁瓣电平（Weighted Integrated Sidelobe Level，WISL）可表示为
式中，w(r,h)为(r,h)处的权重值。令
，最终的优化问题可构造为［12］
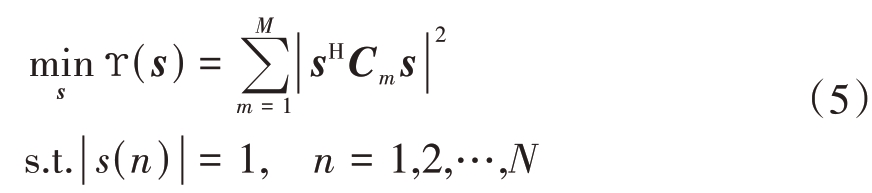
其中，(rm, hm)，m = 1,2,…, M 位于感兴趣的目标区域，M为该目标区域中点的数量。
2 所提方法
式（5）是一个复杂的非线性问题（NP-hard），现有方法一般通过松弛的方式来求解该问题。与现有方法不同，我们利用深度学习神经网络强大的非线性求解能力直接对该问题求解，无需松弛操作。
通过将式（5）转化为无约束的相位优化问题，并将代价函数作为深度学习的损失函数后，式（5）可通过图1所示的深度学习框架进行求解。首先，随机生成归一化的相位序列作为初始输入。然后，前向传播模块中的残差网络输出的优化序列将用于后向传播模块中的损失函数计算。最后，后向传播模块中的Adam 优化器将根据损失函数的计算结果更新残差网络的参数。在整个处理流程中，由于只涉及到波形相位的优化，波形的模值始终保持恒定，因此所提出的方法严格满足CMC。
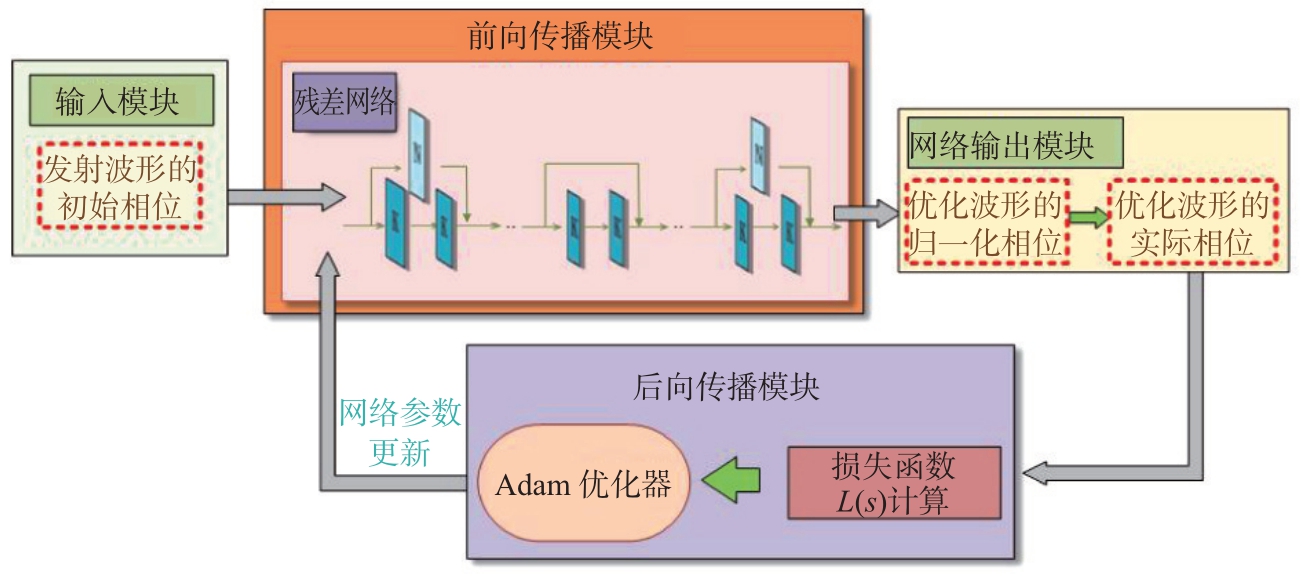
图1 所提的深度学习方法的整体处理框架
2.1 输入模块
由于波形s的相位变化不会对模值产生改变，因此，式（5）中的优化问题可等价转化为下列无约束的相位优化问题：
式中，x ∈ℝN × 1 为波形的归一化相位，表示为x =y/2π，ℝ为实数集，在输入模块中，初始输入x0为随机的归一化相位序列，即x0 ∈( 0,1 ]。
2.2 前向传播模块
为避免因网络层数加深造成的梯度消失和梯度爆炸［13-14］，我们采用残差神经网络来构建前向传播模块，每层网络均采用sigmoid 函数作为激活函数，表示为
对于包含I个残差块的残差网络，第2i-1 层网络（i=1,2,…,I）输出x2i - 1 ∈ℝ1 × h2表示为
式 中，x2i - 2 ∈ℝ1 × h1 为 第i 个 残 差 块 的 输 入，w2i - 1 ∈ℝh1 × h2 和b2i - 1 ∈ℝ1 × h2 分别为该层的权重与偏置向量，h1为输入的维度，h2为第2i-1 层中的神经元个数。
第2i层网络输出x2i ∈ℝ1 × h3，表示为
相似地，w2i ∈ℝh2 × h3 和b2i - 1 ∈ℝ1 × h3 分别为第2i 层的权重与偏置向量，h3为第2i-1 层中的神经元数量，其中，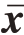
2i - 2 保证了每个残差块输入与输出维度的一致性，表示为
式中，
i ∈ℝh1 × h3和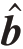
i ∈ℝ1 × h3分别为维度转换层的权重与偏置向量。其中，第1个和第I个残差块，输入和输出的维度不一致。因此，h3分别设置为第1层网络的神经元个数与序列长度N，以确保前向传播的输出与初始信号的维度相同。
假设每个网络层含有K个神经元，输入模块与前向传播模块的结构如图2所示。
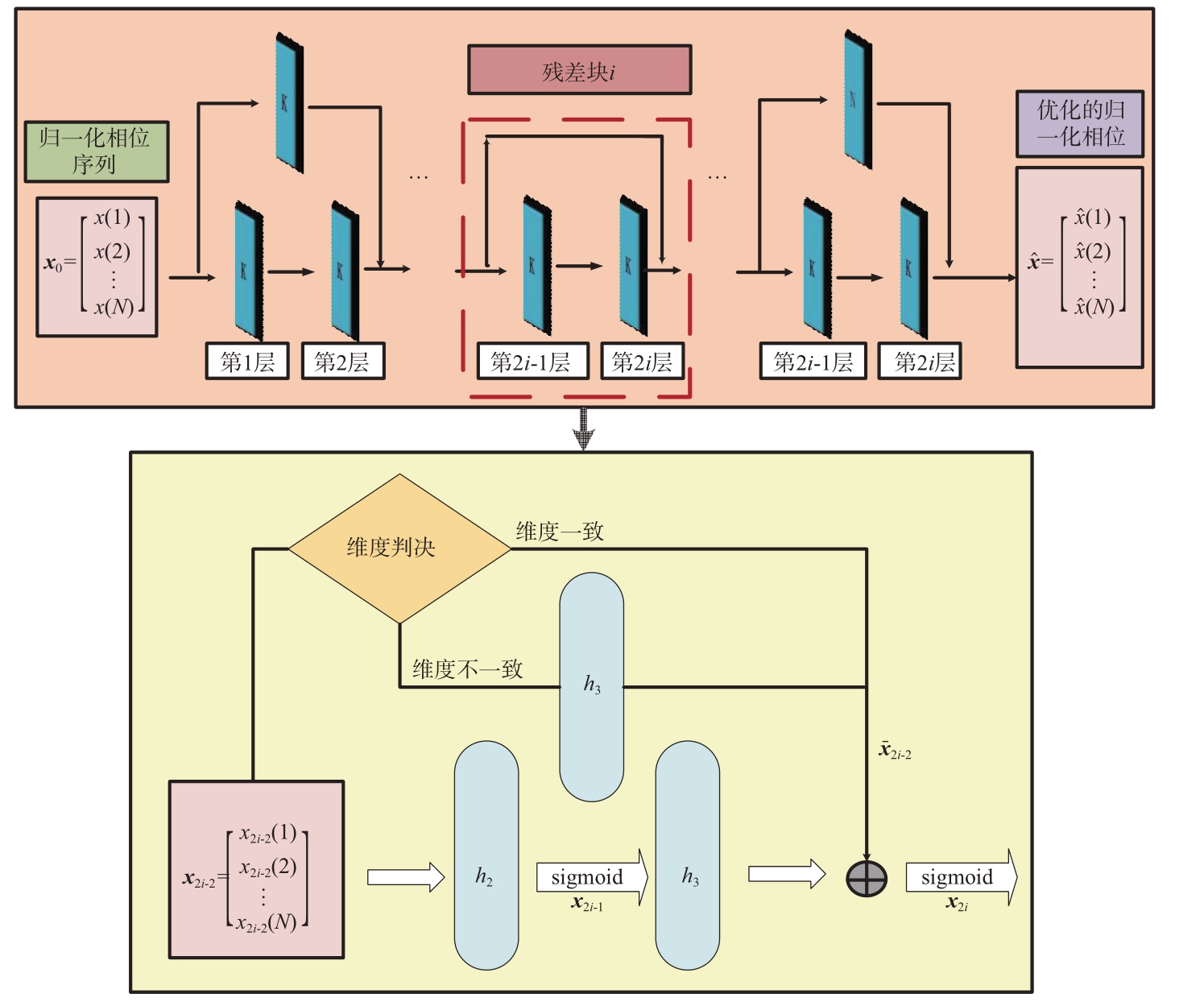
图2 前向传播模块中的残差网络结构
2.3 网络输出模块
经由前向传播模块中的残差网络优化后，输出的归一化相位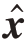
需要在输出模块中转化为实际相位，表示为
，对应的波形
将作为后向传播模块的输入计算损失函数，如图3 所示。图中，L(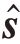
)为后向传播模块中的损失函数。
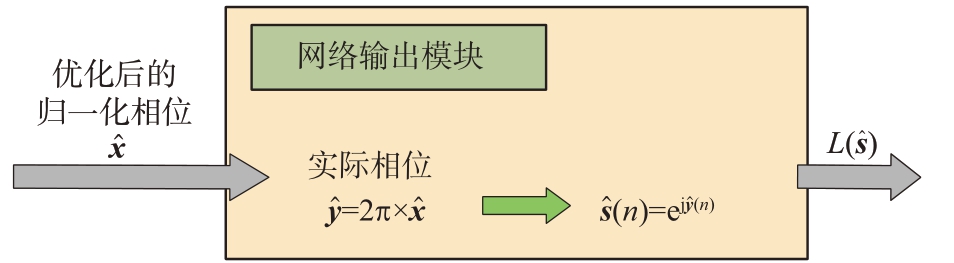
图3 网络输出模块的结构
2.4 后向传播模块
将式（5）中的代价函数ϒ(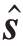
)设置为损失函数L(
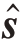)，表示为
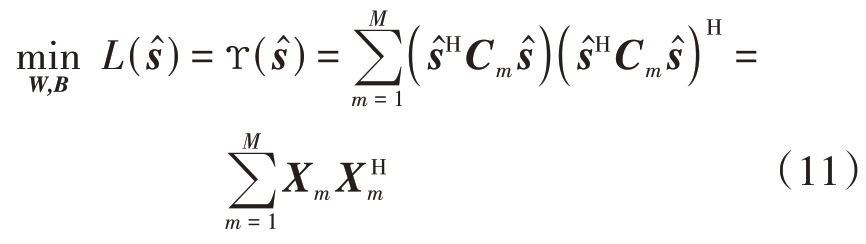
式中，X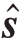m = 
HCm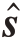
，W,B 是前向传播模块中的网络参数W={w1,w2,…,w2I}⋃{
1,
I}和B={b1,b2,…,b2I}⋃{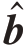
1,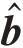
I}。由于深度学习神经网络是实值网络，只能对实数优化，需要对式（11）中的变量实虚分离后才能计算损失函数，式（11）可重新构造为
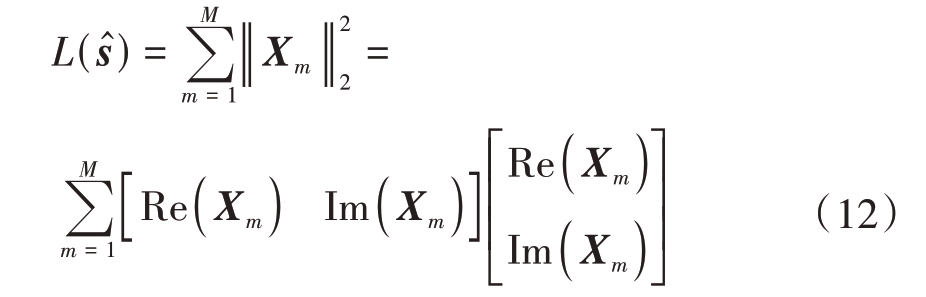
式中，Re(·)表示矩阵/向量的实部，Im(·)表示矩阵/向量的虚部，计算Xm 所涉及的实虚分离操作分别为
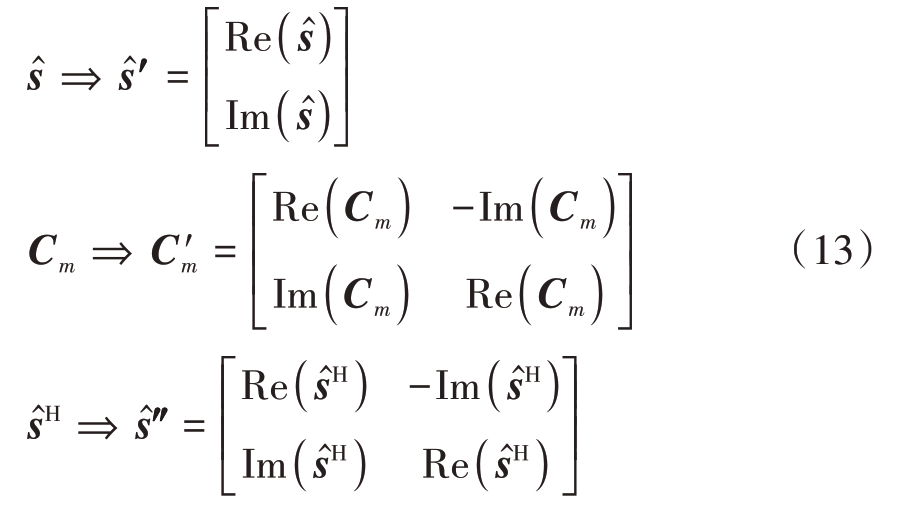
在式（13）的基础上，
，其中，Re( Xm )和Im( Xm )可分别由实数运算式（14）和式（15）得到：
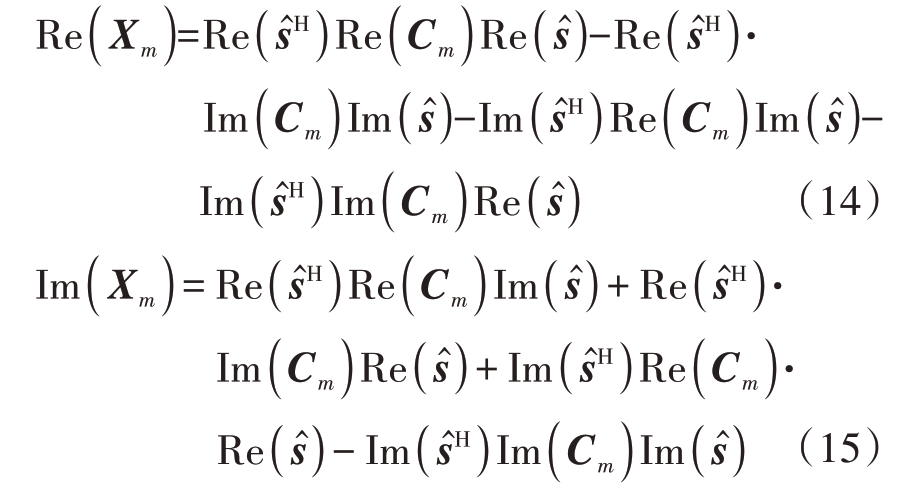
根据损失函数计算结果，Adam 优化器将对W,B 进行优化，并对前项传播模块中的网络参数进行更新，后向传播模块的结构如图4所示。
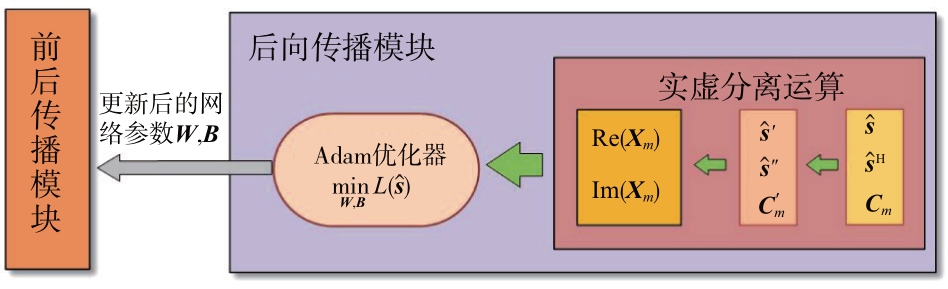
图4 后向传播模块的处理流程
3 仿真结果
在本节中，我们对所提方法在目标区域的WISL 的抑制性能和目标探测性能与文献［9］中的CIAFIS算法以及文献［12］中的QGD算法进行了对比。3 种方法的初始输入均为长度N=50 的恒模随机相位序列，多普勒频点个数为Nv=50，w(r,h)设置为
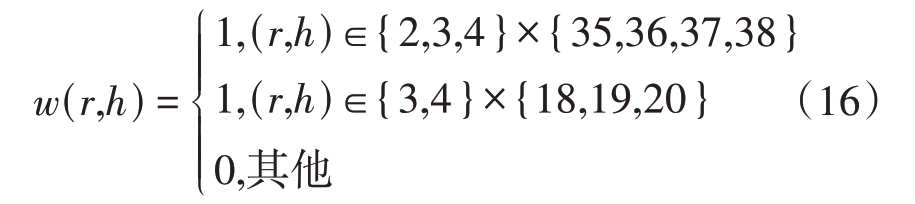
网络参数方面，残差网络的残差块个数I=3，每个网络层包含128 个神经元，学习率设置为0.000 1，最大迭代次数D=1 000。
3.1 WISL抑制性能
图5 展示了CIAFIS，QGD 以及所提方法的模糊函数图，图中的红色矩形框标注了w(r,h)中设定的目标区域。如图所示，3 种方法均能有效地在目标区域处的旁瓣进行抑制。在3种方法中，所提算法可形成120 dB 以下的凹口，其他两种方法均未达到该水平。
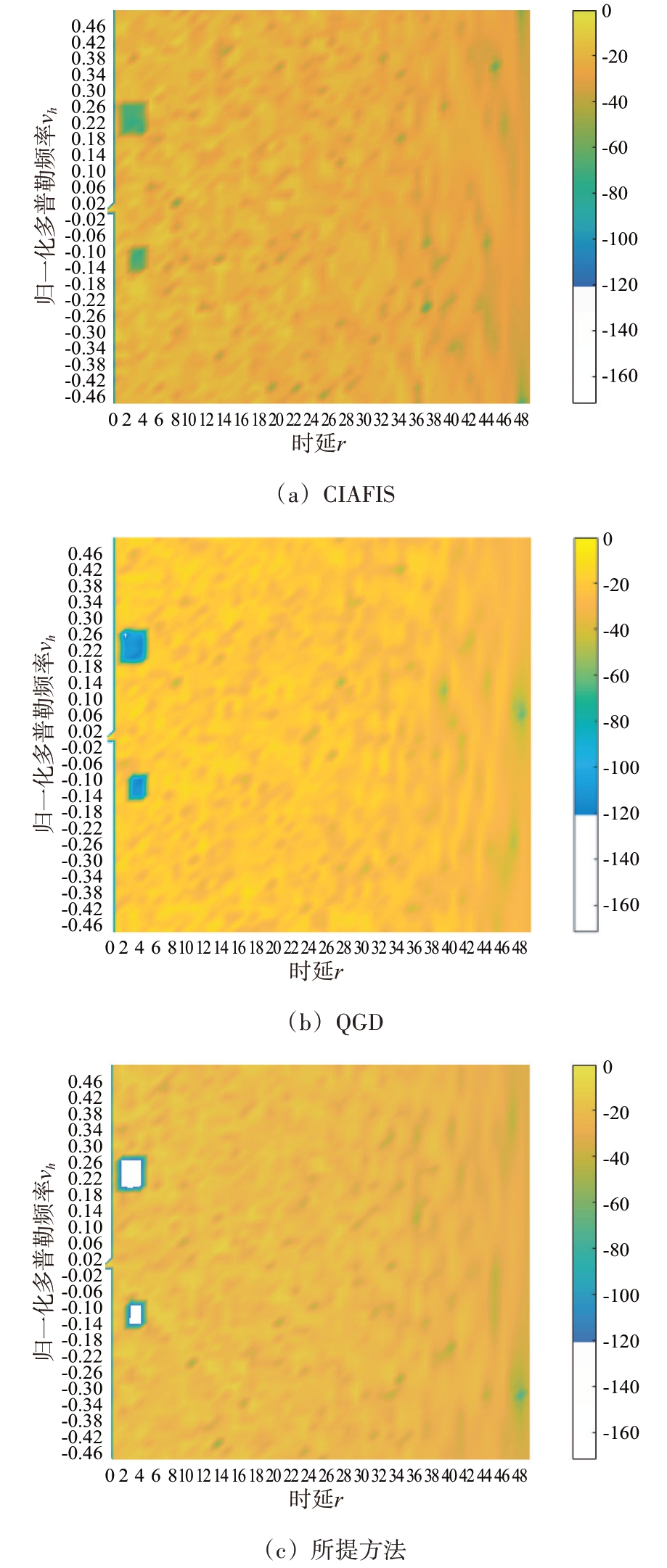
图5 CIAFIS，QGD与所提算法的模糊函数图
图6 是3 种算法在r=2, r=3 和r=4 处的模糊函数切片，更加具体地描述了3 种算法对目标区域WISL 的抑制能力，可以看到所提算法在3 个距离切片处的模糊函数值均低于CIAFIS 与QGD，分别比CIAFIS和QGD低了70 dB和20 dB左右。
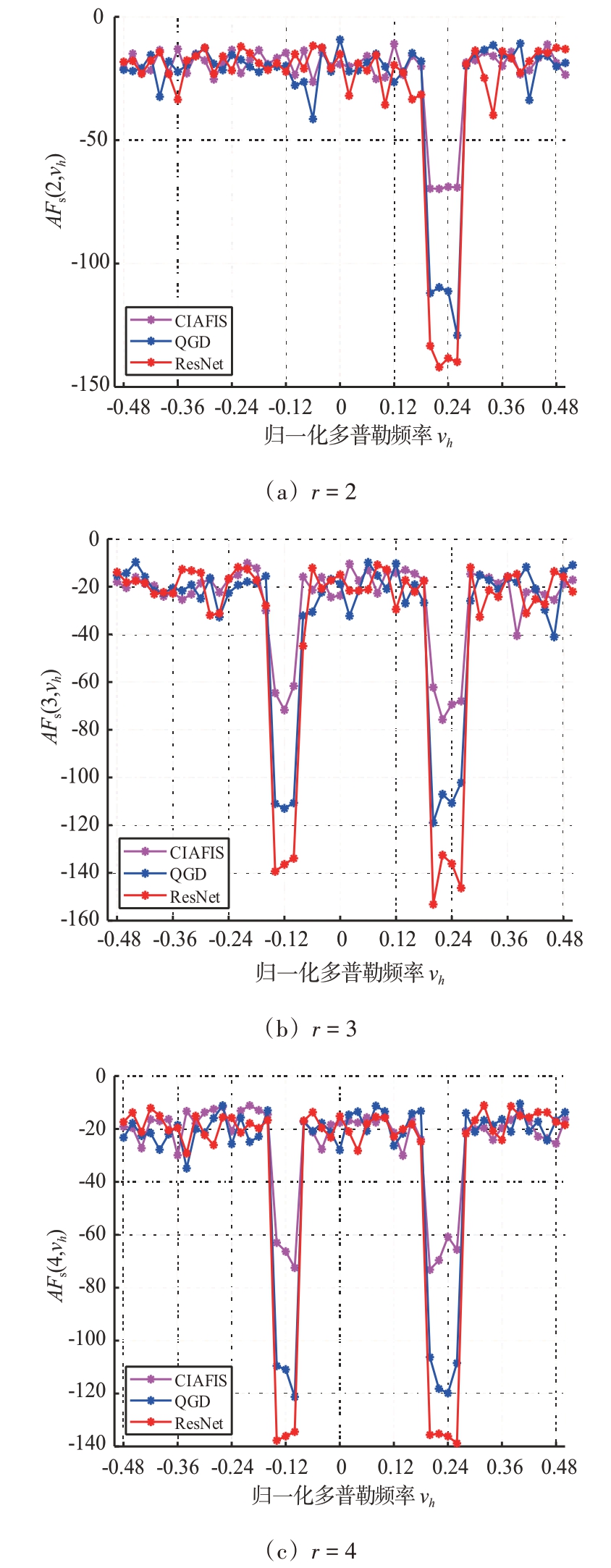
图6 r = 2,3,4处的模糊函数切片图
另外，我们对比了该场景下3种方法的SIR，表示为
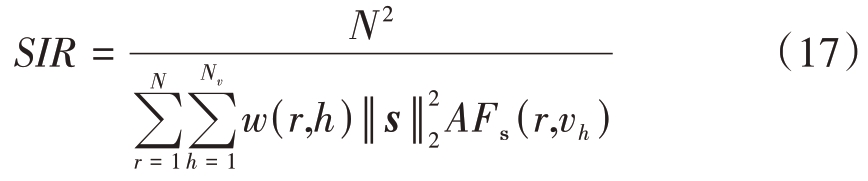
如表1所示，所提方法的SIR 分别比CIAFIS 和QGD 方法高了70.47 dB 和26.86 dB，体现了所提方法对WISL强大的抑制能力。
表1 CIAFIS，QGD与所提方法的SIR
CIAFIS 53.42 dB QGD 97.03 dB所提方法123.89 dB
图7 展示了3 种算法的代价函数随迭代次数变化的曲线。可以看到所提算法在1 000 次迭代后即可达到收敛值3.635 × 10-8，该数值分别比QGD与CIAFIS分别低了2个和8个数量级，而这两种对比算法的迭代次数均高于所提算法，证明了所提算法拥有更好的收敛性能。
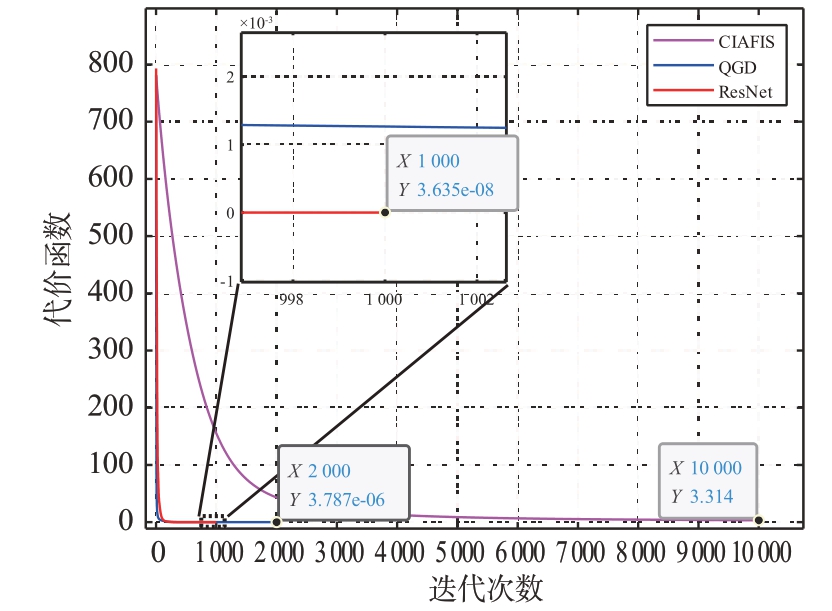
图7 3种算法的代价函数下降曲线
3.2 目标探测性能
考虑在1 个速度为320 m/s，距离为100 km 的强目标，同时考虑1个弱目标，速度为1 200 m/s，距离为100.5 km，两者的回波强度分别为30和-25 dB。图8 展示了3 种方法得到的优化序列在噪声功率σ2 分别为-40 dB 和-10 dB 时的目标探测效果。如图8（a）与图8（e）所示，初始序列仅能对强目标有效探测，而弱目标则被强目标的回波旁瓣所遮掩。如图8（b）～（d）所示，噪声功率为-40 dB 时，3 种方法均能探测到强目标和弱目标，其中，QGD 与所提算法的分辨率要强于CIAFIS 方法。如图8（f）～（h）所示，当噪声功率上升到-10 dB，CIAFIS 方法已经无法有效识别到弱目标，QGD 对弱目标的探测分辨率也有所下降，而所提算法仍然可以清晰地探测到弱目标，该结果表明，所提方法具有更强的目标探测性能。
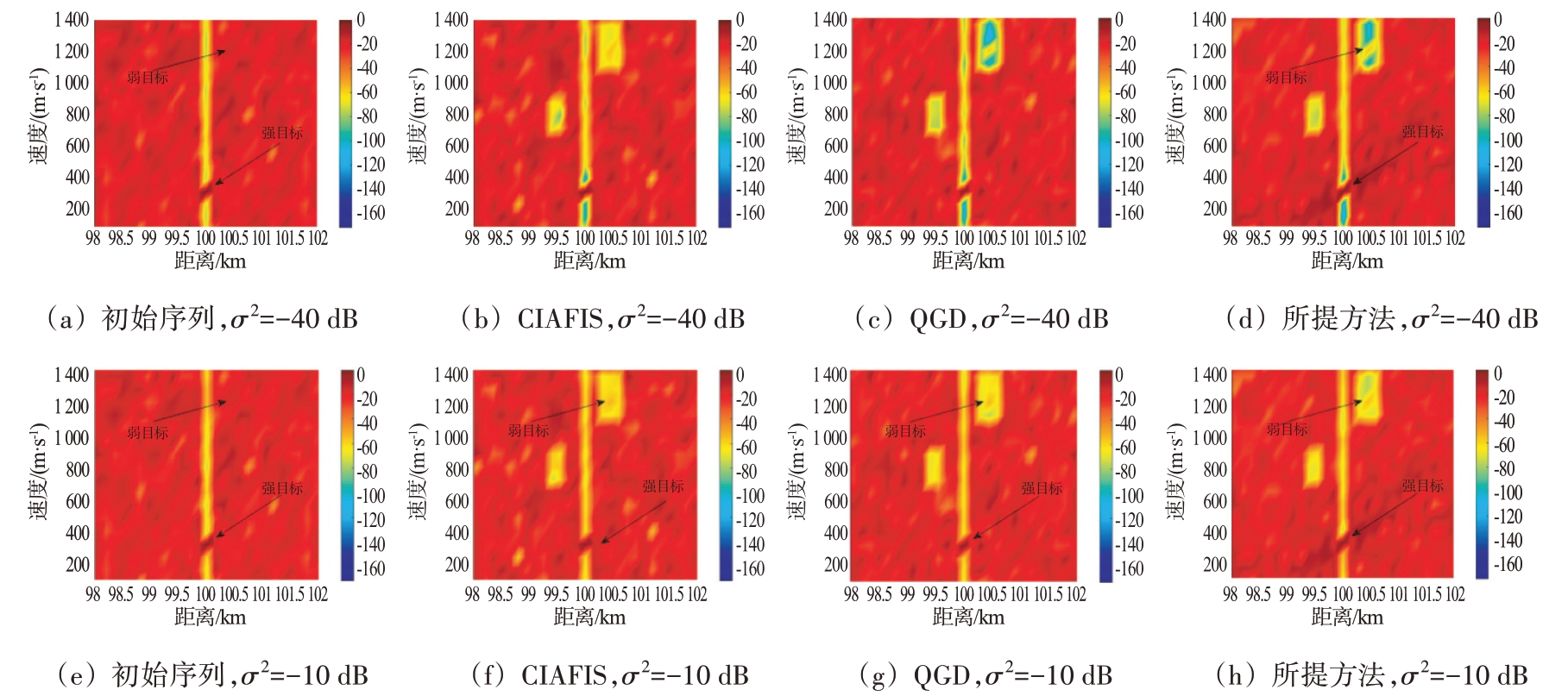
图8 不同噪声功率下3种算法的目标探测性能
4 结束语
本文对发射波形的模糊函数赋型进行了研究。该问题是一个恒模约束下的非线性问题（NPhard）。现有方法往往需要对该问题进行松弛。为了解决该问题，我们利用深度学习残差神经网络强大的非线性优化能力，提出了一种无需松弛的模糊函数赋型方法。首先，我们将该问题转化为一个无约束的相位优化问题。然后，我们将该问题的非凸目标函数构造为网络的损失函数。最后，使用残差网络直接对波形的相位进行优化。仿真结果表明，所提算法有着更强的WISL 抑制性能，并能有效提升雷达系统对弱目标的探测能力。
［1］ 杨晨，吴蕾，杨威，等.基于分式二次规划的互模糊函数赋形方法［J］.雷达学报，2024，13（1）：174-186.
［2］ YI Haoyu , JING Weidong, ZHANG Xinyu, et al.Quartic Optimization for Ambiguity Function Shaping via RTR Algorithm under ADPM Framework［C］//2022 IEEE 22nd International Conference on Communication Technology,Nanjing, China:IEEE, 2022:1060-1064.
［3］ YANG Jing, CUI Guolong, YU Xianxiang ,et al.Cognitive Local Ambiguity Function Shaping with Spectral Coexistence［J］.IEEE Access, 2018, 6:50077-50086.
［4］ WANG Fulai, FENG Sijia, YIN Jiapeng, et al.Unimodular Sequence and Receiving Filter Design for Local Ambiguity Function Shaping［J］.IEEE Trans on Geoscience and Remote Sensing, 2022, 60:1-12.
［5］ ZHANG Cui, PEI Jifang,ZHANG Yujie,et al.Slow-Time Ambiguity Function Shaping with Spectral Coexistence for Cognitive Radar［J］.IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2023,16:8418-8430.
［6］ QIU Xiangfeng, YANG Chen, JIANG Weidong, et al.Joint Design of Transmit Waveform and Receive Filter for Cross Ambiguity Function Synthesis［J］.IEEE Wireless Communications Letters, 2024，13（3）:839-843.
［7］ CUI Guolong, FU Yue, YU Xianxiang, et al.Local Ambiguity Function Shaping via Unimodular Sequence Design［J］.IEEE Signal Processing Letters, 2017, 24（7）:977-981.
［8］ 徐乃清，张劲东，李晨，等.基于MM 算法的脉冲串模糊函数设计方法［J］.雷达科学与技术，2020，18（6）:599-604.
［9］ WU Linglong, BABU P, PALOMAR D P.Cognitive Radar-Based Sequence Design via SINR Maximization［J］.IEEE Trans on Signal Processing, 2016, 65（3）:779-793.
［10］ YANG Jing, CUI Guolong, YU Xianxiang, et al.Dual-Use Signal Design for Radar and Communication via Ambiguity Function Sidelobe Control［J］.IEEE Trans on Vehicular Technology, 2020, 69（9）:9781-9794.
［11］ QIU Xiangfeng, JING Weidong, ZANG Xinyu, et al.Quartic Riemannian Trust Region Algorithm for Cognitive Radar Ambiguity Function Shaping［J］.IEEE Geoscience and Remote Sensing Letters, 2022, 19:1-5.
［12］ ALHUJAILI K, MONGA V, RANGASWAMY M.Quartic Gradient Descent for Tractable Radar Slow-Time Ambiguity Function Shaping［J］.IEEE Trans on Aerospace and Electronic Systems, 2020, 56（2）:1474-1489.
［13］ HU Jinfeng, WEI Zhiyong, LI Yuzhi, et al.Designing Unimodular Waveform（s） for MIMO Radar by Deep Learning Method［J］.IEEE Trans on Aerospace and Electronic Systems, 2021, 57（2）:1184-1196.
［14］ ZHONG Kai, HU Jinfeng, PAN Cunhua.Constant Modulus MIMO Radar Waveform Design via Iterative Optimization Network Method［J］.IEEE Trans on Instrumentation and Measurement, 2023, 72:1-11.