0 引 言
2024 年两会上,“低空经济”首次被列入政府工作报告,年底国家发改委低空经济发展司正式挂牌,开启了空中飞行活动发展规划的新节点。在各类航空飞行器中,浮低空飞行器以其滞空工作时间长、使用效费比高等优势,近年来被广泛应用于航拍航测、应急救援及城市公共服务中,为社会经济发展做出重要贡献。然而随着该类飞行器使用频次的日益上升,其与其他各类飞行活动产生的复杂空中交通流［1］给空域管理带来严峻的挑战。如何对各类航空器进行有效地跟踪、识别和分类,提升空域态势感知能力并促进航空事业的健康持续发展,一直是空管部门和研究人员关注的热点。
由于目标识别分类与其运动特性、电磁散射特性乃至结构外形等各类信息的获取紧密相关［2-3］,因此目标运动状态及其外形参数的估计显得尤为重要。目前,浮低空飞行器大多依赖充盈惰性气体作为浮升动力,使得其结构体积较为庞大,外形尺寸也随之扩展增大。因而随着测量设备如高频段雷达分辨能力的不断提升,该类飞行器呈现电大目标电磁散射特性,具有变化的多散射中心及单时间帧内产生多个雷达量测的特点［4］。在此情况下,传统基于“点目标”及目标与量测“一对一”关联假设的滤波处理算法面临局限性,而将其视为具有一定形态（含形状、大小、方向）的“扩展目标”开展雷达多量测跟踪更趋合理。
当前,有关扩展目标跟踪的研究方法中应用最广的是文献［5］提出的随机矩阵模型,其采用对称正定的随机矩阵将目标扩展外形表示为一个椭圆（体）,并将该扩展外形矩阵与运动状态一起作为目标跟踪的联合状态变量,从而在贝叶斯滤波框架下实现了对扩展目标两类状态后验概率密度的联合估计。随后,文献［6-7］相继改进了原始随机矩阵模型中未考虑回波散射点位置不确定性、传感器测量误差、扩展外形随时间演化以及测量失真等不足,进一步提高了随机矩阵模型的准确性与鲁棒性,夯实了其应用的理论基础。文献［8］提出了椭圆随机超曲面模型,相比于随机矩阵模型,椭圆随机超曲面模型对扩展目标的估计精度更高,但其预设方程多、计算成本高。另外,对于一些不太符合椭圆（体）形状的扩展目标跟踪来说,随机矩阵模型的估计精度遇到挑战。针对该不足,文献［9-10］利用多椭圆拟合的随机矩阵模型对目标扩展近似建模,并借助多模型跟踪及变分贝叶斯等方法,实现了该类目标联合状态的良好估计。此外,也有学者利用基于随机超表面模型的星凸外形建模［11-12］、基于高斯过程学习的任意形状建模［13-14］,进一步增强了对扩展外形不确定性的适应能力。但是,越精细的扩展目标外形建模通常伴随复杂的扩展目标跟踪理论实现,从工程应用来说仍需结合实际场景加以注意选择。
本文以空管高分辨雷达跟踪识别具有扩展形态的浮低空飞行器为背景,为提高该类目标跟踪及其外形参数估计的精度,基于该类飞行器结构主体大多具有旋转对称形式、外形近似为椭圆体的特点,以及考虑描述椭圆（体）的随机矩阵模型具有原理简单、鲁棒性强等优点［4-7,9-10］,采用随机矩阵模型建模飞行器的扩展外形并开展滤波估计,利用特征值分解方法估算其外形参数,对低空态势感知及空域管理具有重要的支撑作用。
1 飞行器跟踪系统模型
1.1 扩展状态模型
在随机矩阵理论中,记k - 1 时刻目标扩展状态为d × d（本文飞行器位三维空间,即d = 3）维的对称正定随机矩阵Xk - 1,并假设Xk - 1 的后验概率密度服从逆威沙特（Inverse Wishart, IW）分布
式中,Zk - 1 为第1 至k - 1 时刻累积获得的传感器量测集,vk - 1|k - 1为IW 分布的自由度,满足vk - 1|k - 1 -2d - 2 > 0,Vk - 1|k - 1 > 0 为d × d 维参数矩阵,且由IW 分布IW(Y; b,C)的期望
可知
假设目标扩展状态与运动状态的演化相互独立,且扩展状态的演化服从威沙特（Wishart, W）分布
式中,δk|k - 1 ≥d 为W 分布的自由度参数,用于描述扩展状态时间演化的不确定性。
1.2 运动状态模型
记k - 1时刻目标质心运动状态xk - 1为后验概率密度服从高斯（Gaussian, G 或N）分布的状态向量,即
式中：x =[p,v,a ]为单个维度空间的目标质心状态变量,p 表示位置,v 表示速度,a 表示加速度；xk - 1|k - 1 为高斯分布状态的后验期望值；Pk - 1|k - 1 为其期望误差协方差矩阵。
采用Singer 模型［5］建立目标运动状态演化模型
式中,状态转移（或演化）矩阵Φk|k - 1、高斯过程白噪声wk的协方差矩阵Q分别为
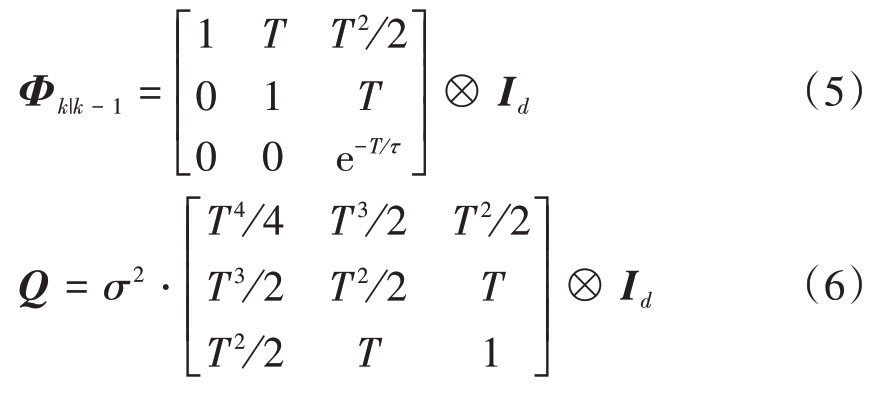
式中,T 为雷达采样周期,τ 为时间常数,Id 为d × d维的单位向量矩阵,σ 为过程噪声系数,⊗表示Kronecker乘积。
1.3 雷达测量模型
记k 时刻由nk 个雷达量测组成的目标量测集为
为便于后续分析,假设
为服从高斯分布的等效位置量测。文献［6］考虑了传感器测量噪声和目标扩展对量测分布的共同影响,给出测量模型
式中
为测量矩阵
为单维状态空间的测量矩阵
为零均值等效位置测量噪声,Rk 为传感器测量噪声协方差矩阵,λ 为描述扩展状态Xk 影响的尺度因子,若假设量测服从正态分布,则取λ = 1,若服从均匀分布,则
那么,量测似然可表示为
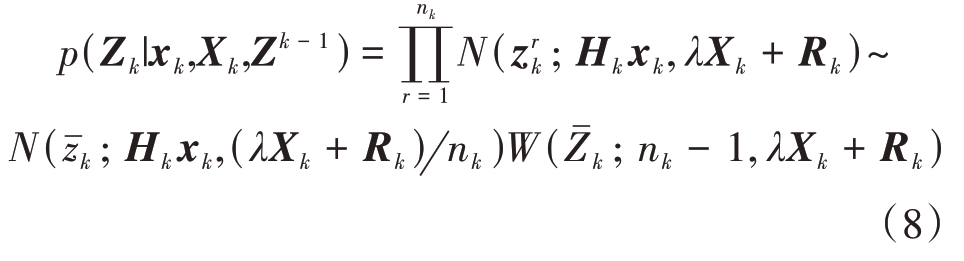
式中,量测质心
量测散射矩阵
分别为
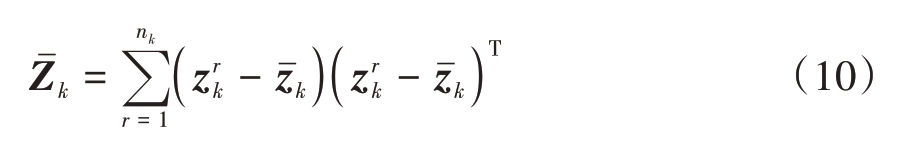
2 飞行器跟踪估计方法
2.1 基于高斯逆威沙特分布滤波的飞行器状态估计
在贝叶斯（Bayes）滤波框架［15］下,通过计算目标运动状态xk、扩展状态矩阵Xk 的高斯逆威沙特分布联合后验条件概率密度函数
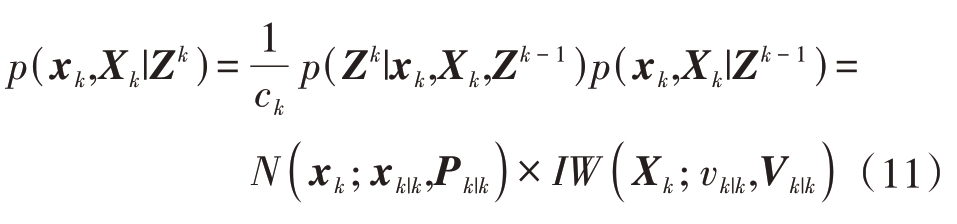
实现目标联合状态(xk,Xk)的估计,其中ck 为概率函数归一化因子。可以看出,飞行器的状态跟踪估计分为时间更新、测量更新两个步骤。
步骤1 时间更新
k-1时刻,基于累积量测集Zk-1={Z1,Z2,…,Zk-1}对k时刻的飞行器联合状态进行预测
因此,联合状态一步预测可分解为以下两部分：
1） 扩展状态预测
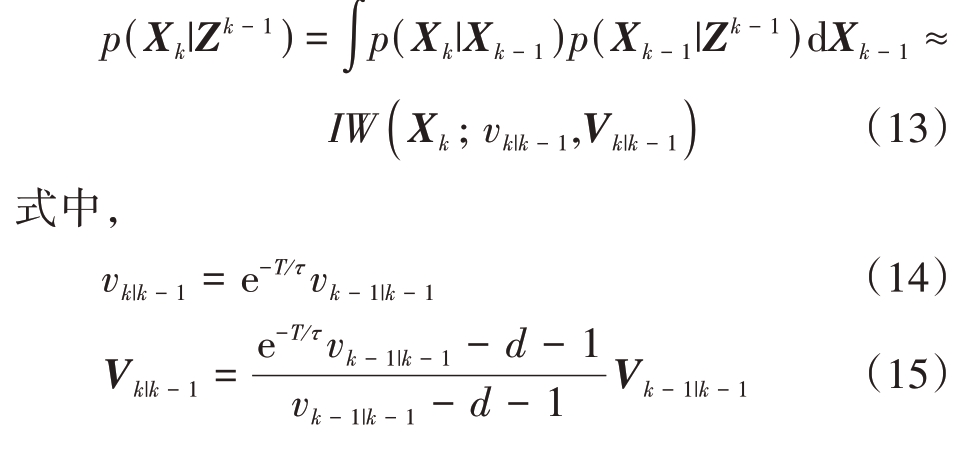
从而由IW分布期望可知扩展状态预测为
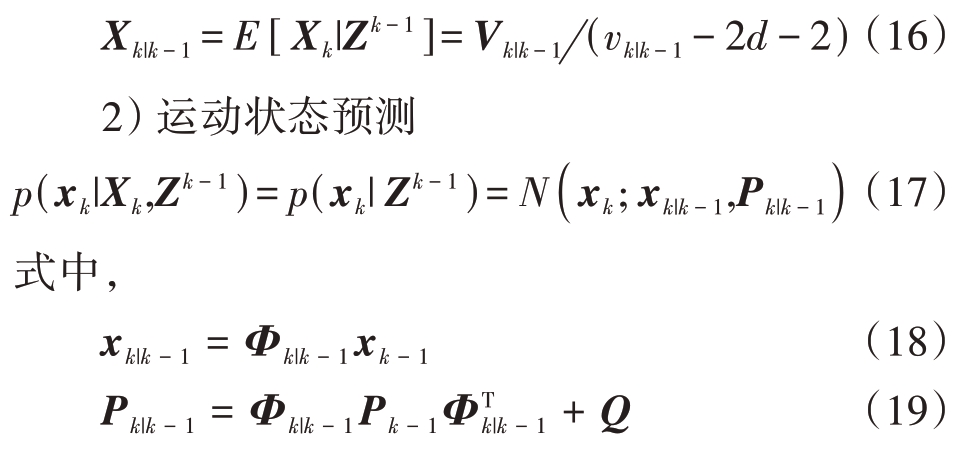
步骤2 测量更新
k 时刻,获得量测集
形成累积量测集Zk后,对飞行器联合状态进行更新
因此,联合状态测量更新可分解为以下两部分：
1） 扩展状态更新
式中,
其中,
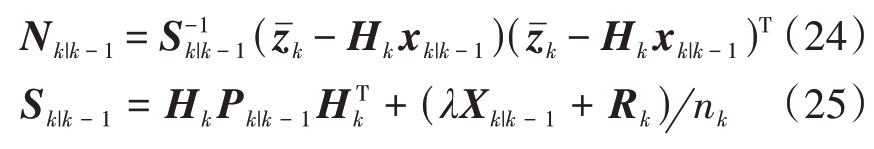
从而可知扩展状态更新为
2） 运动状态更新
式中,
其中,
2.2 基于特征值分解的飞行器扩展外形参数估计
基于随机矩阵模型建模并滤波可以估计任意k 时刻椭圆（体）形状目标的扩展外形矩阵,但该矩阵估计Xk|k 无法直观地描述该时刻椭圆（体）方向和半轴长度（Orientation and Half Axes Lengths of an Ellipse, OAL）,而这些信息在扩展目标的识别和分类中往往是必要的［16］。由1.3 节测量模型可知,在矩阵迹trace（Xk）≫trace（Rk）的一般条件下,扩展状态Xk可作为飞行器质心位置状态观测不确定性的协方差矩阵描述,同时该矩阵也包含了其近似椭圆体扩展外形的空间特征信息。事实上,一个任意大小及指向的椭圆（体）均可以用OAL 特征参数来描述,同时基于空间样本点估计的协方差矩阵［17］均可以通过其特征值及特征向量表征,如图1所示。
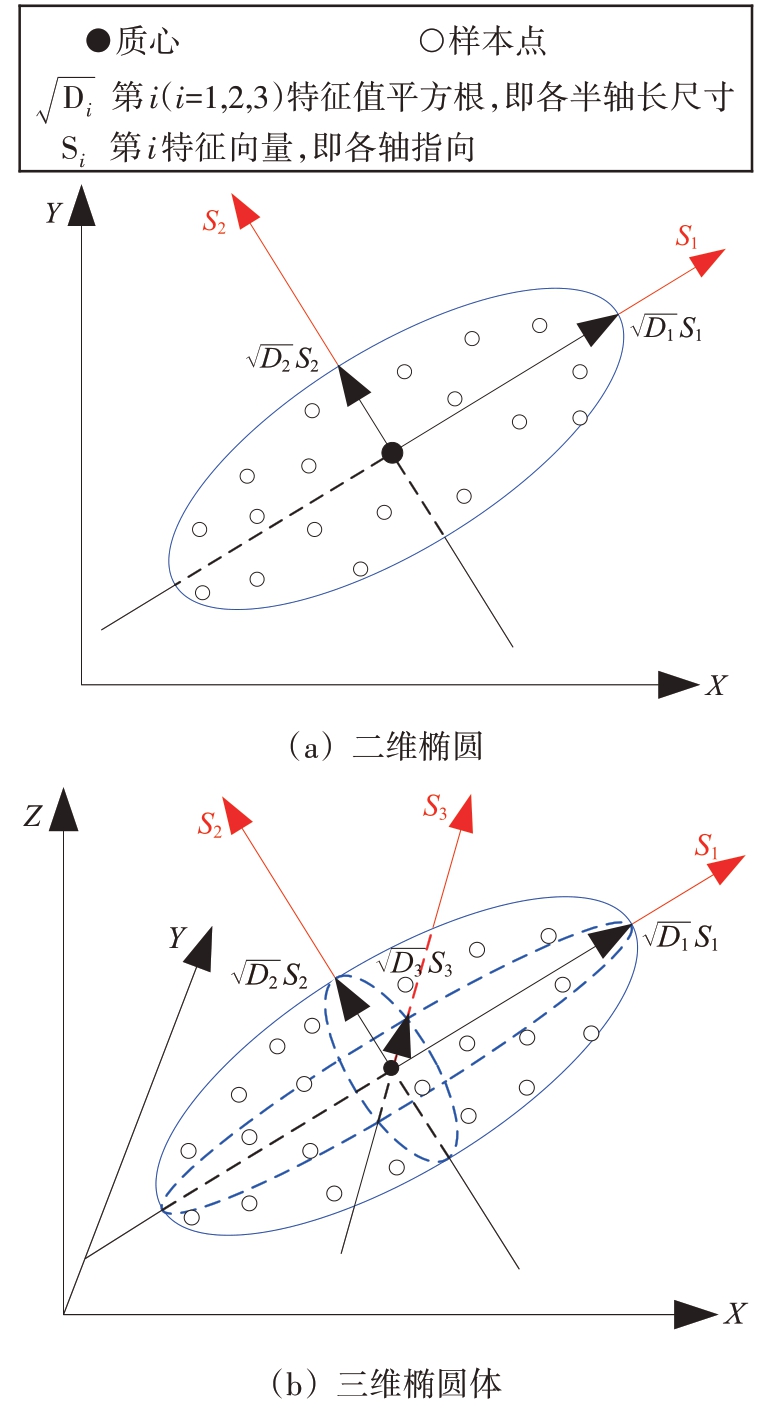
图1 椭圆（体）外形参数示意图
鉴于此,本文使用特征值分解方法［18］对Xk|k 进行特征提取,将提取的特征值平方根及最大特征值对应的特征向量分别作为飞行器的半轴长尺寸及主轴方向,从而实现对其外形参数的在线估计,如表1所示。
表1 基于特征值分解的扩展外形参数估计伪代码
输入：k时刻飞行器扩展状态矩阵估计Xk|k 1. [S,D]= eig(Xk|k)2. ς̂min k =sqrt(D2) + sqrt(D3)2 3. ς̂maj k = sqrt(D1)4. ς̂OR k = S1输出：k时刻飞行器短半轴长估值ς̂min k ,长半轴长估值ς̂maj k ,主轴方向ς̂OR k
3 仿真实验
本文着重讨论雷达不同测量精度、量测数目条件下,所提方法对浮低空飞行器质心运动状态及其扩展外形参数的估计性能。下面给出仿真实验参数设置及估计评价指标。
3.1 参数设置
对空管雷达,假设采用多部异地分置的相同高分辨率雷达跟踪上述飞行器,以降低单部雷达探测角度的局限性及保证量测数据量的一定冗余性［4］,并将所有雷达量测数据汇集至空管数据中心进行融合滤波处理以实现飞行器状态跟踪估计。雷达采样周期取T = 1 s。雷达测量精度（即测量方差）按5 倍递增的标准差恶化趋势设置3 种不同级别,分别为R1 = 0.22Id(m2),R2 = 12Id(m2),R3 =52Id(m2),以比较不同雷达测量精度对飞行器联合状态跟踪及外形参数估计效果的影响。此外,为便于比较不同融合量测数目下飞行器联合状态及其外形参数的估计效果,取3组不同的确定性融合量测数目,分别为Num1 = 10,Num2 = 16,Num3 = 22。本文假设量测服从正态分布,并取尺度因子λ = 1［6］。
对浮低空飞行器,假定其近似椭圆体的主体扩展外形的短半轴长度ςmin = 5 m,长半轴长度ςmaj = 12 m,低空平飞轨迹高度维持在距地面300 m,且假设飞行器速度方向与主轴指向保持一致。图2所示以每隔3个采样步长的方式清楚展示了在以上述其中某台空管雷达为参考建立的雷达站心坐标系下的浮低空飞行器航迹。图3 展示了某时刻飞行器的扩展外形及雷达量测空间分布情况,其中坐标轴XB 代表飞行器主轴,黑色椭球体表示飞行器的真实扩展外形,红色+点表示雷达等效位置量测点,由于雷达测量噪声及飞行器扩展外形的共同影响,量测点在飞行器质心附近呈正态散布。
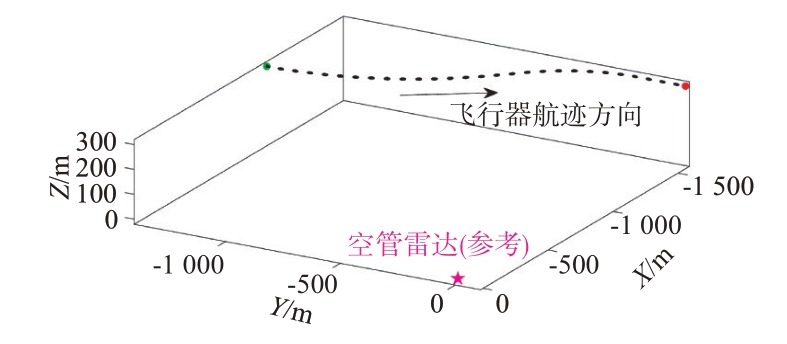
图2 浮低空飞行器飞行示意图
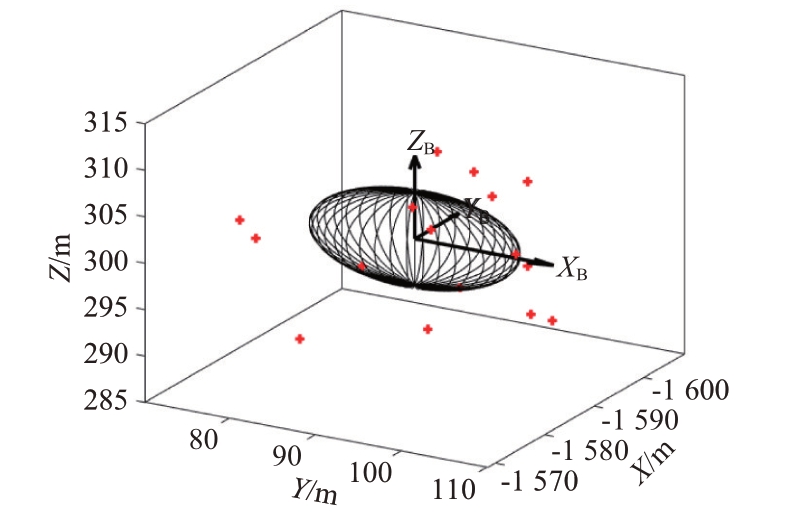
图3 飞行器扩展外形及雷达量测分布示意图
对高斯逆威沙特分布滤波的运动状态模型,滤波位置初值可取作初始采样时刻等效位置量测质心,滤波速度初值依前2个采样时刻量测质心作差分获得,质心运动状态协方差矩阵初值取P0 =diag([25 1 0.25])⊗Id,时间常数取τ = 0.1。对扩展状态模型,扩展外形矩阵初值X0 可取作初始时刻等效位置量测集的量测散射矩阵,其所服从IW分布的自由度初值及参数矩阵初值可分别按式v0 = 2d + 2 + 1 和V0 =(v0 - 2d - 2)X0 获得,过程噪声系数取σ = 0.1。
3.2 评价指标
采用均方根误差（Root Mean Square Error,RMSE）评估本文滤波方法对飞行器质心位置状态、速度状态的估计性能,并取蒙特卡洛仿真运行次数Ns = 200。
式中,下标l 表示第l 次蒙特卡洛运行过程
分别表示当前运行k时刻飞行器质心位置状态（真值
速度状态（真值
）的估计值
表示求取2范数。
采用平均估计误差（Average Estimation Error,AEE）评估本文滤波后特征值分解方法对飞行器扩展外形参数的估计性能
式中
分别为当前运行k 时刻飞行器扩展外形参数长半轴长度（真值ςmaj）、短半轴长度（真值ςmin）、主轴方向（真实方向
）的估计值。
4 结果分析
4.1 质心运动状态估计
首先,以测量精度R2、融合量测数目Num2 为例分别给出单次蒙特卡洛仿真运行中飞行器X、Y、Z 三个方向的质心位置状态、速度状态的滤波结果,如图4、图5所示。为了能较清晰地对比滤波值与实际真值,两图中均对滤波值等间隔选取4个雷达采样步长予以展示。
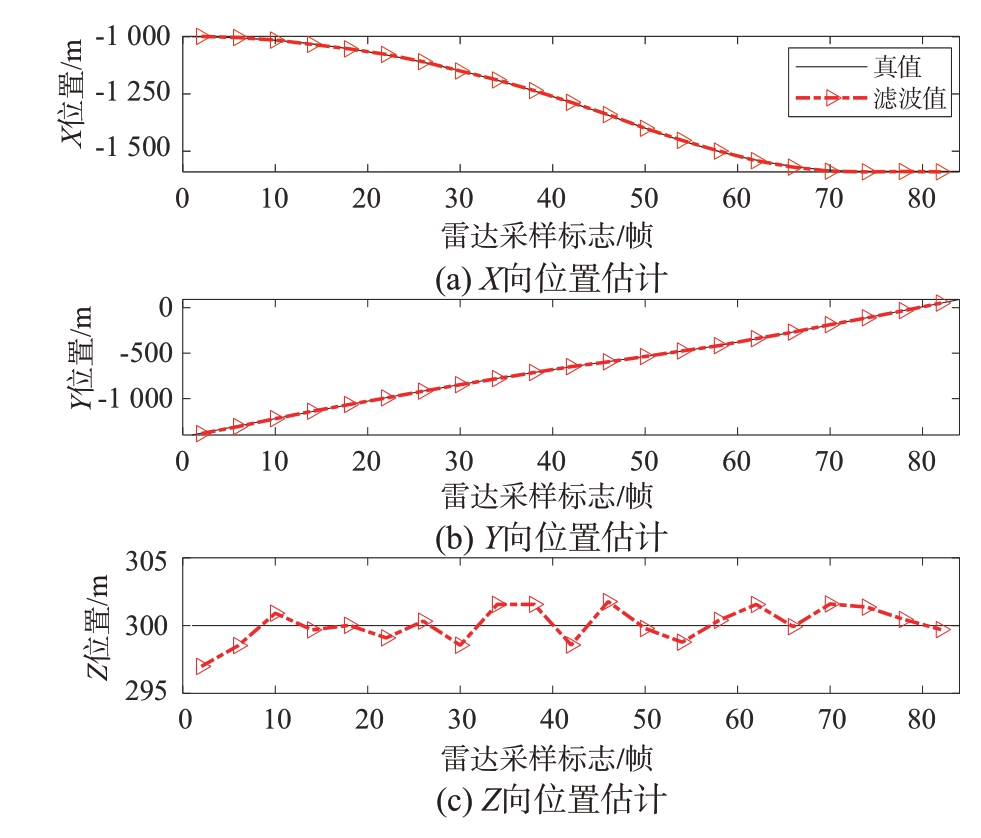
图4 质心位置状态估计结果
图5 质心速度状态估计结果
可以看到,由于位置状态以初始时刻雷达等效位置量测集的量测质心作为滤波初值,故各方向的质心位置状态估计值可以快速地收敛于真值附近；然而速度状态滤波初值依前2个采样时刻量测质心作差分获得,其与实际真值存在一定偏差,使得相应方向的滤波估计速度值在初始阶段产生一定偏差,但在经过初始滤波振荡后,各方向的质心速度估计值均能基本收敛于速度真值,且与后者存在一定的滤波估计误差。此外,图6展示了单次运行中第50 至52 帧飞行器扩展外形状态的估计效果,其中黑色椭球体为飞行器真实的扩展形态,红色椭球体为本文方法估计出的飞行器形态,可以看到估计的飞行器扩展形态与其真实形态能较好地产生重叠,说明基于随机矩阵建模的飞行器跟踪方法对其扩展状态具有较好的估计性能,验证了该方法的有效性。
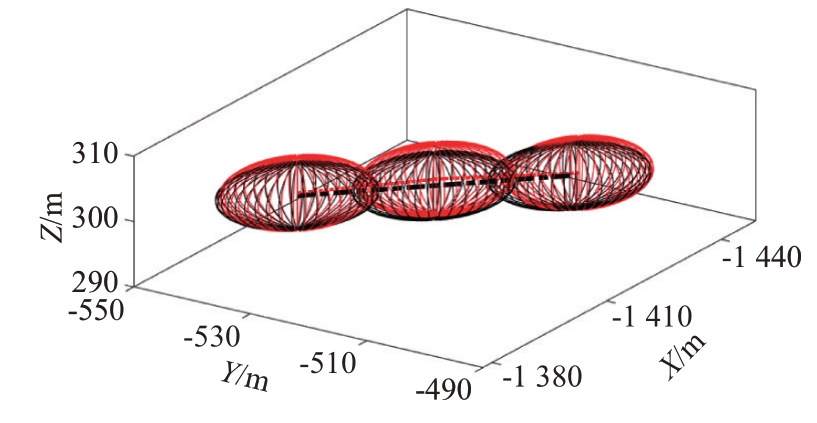
图6 扩展状态估计结果局部展示
其次,表2给出了在3.1节所设不同测量精度、融合量测数目下,200 次蒙特卡洛运行的飞行器质心运动状态（位置、速度）的估计RMSE。可以看到,随着测量精度的提升以及融合量测数目的增加,基于随机矩阵模型建模的飞行器运动状态估计精度基本上都得到提升,因为测量精度的上升意味着高分辨雷达的测量不确定性减小,等效位置量测的空间分布更接近于目标真实扩展,从而有利于保证量测质心（亦即飞行器质心）运动状态的滤波精度,而融合量测数目的增加意味着获取目标信息量的增加,从滤波跟踪算法的角度来说这对提升滤波估计精度同样大有裨益。然而,实际雷达目标跟踪过程中随着探测相对几何的变化,雷达测量精度及量测数目均会发生较大的变化,从而可能造成滤波精度的不稳定,而本文这里只是对比和讨论这种确定性的变化假设条件对估计精度造成的影响。
表2 不同测量精度、融合量测数目下的质心运动状态估计RMSE对比
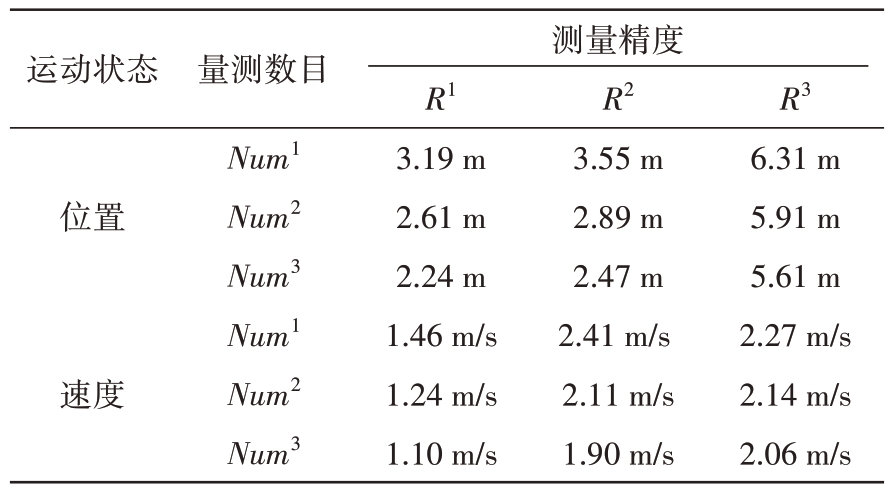
运动状态位置速度量测数目Num1 Num2 Num3 Num1 Num2 Num3测量精度R1 3.19 m 2.61 m 2.24 m 1.46 m/s 1.24 m/s 1.10 m/s R2 3.55 m 2.89 m 2.47 m 2.41 m/s 2.11 m/s 1.90 m/s R3 6.31 m 5.91 m 5.61 m 2.27 m/s 2.14 m/s 2.06 m/s
4.2 扩展外形参数估计
以测量精度R2、融合量测数目Num2 为例,图7展示了单次仿真运行时本文特征值分解方法与文献［19］中最小二乘拟合方法对飞行器短半轴长度、长半轴长度等扩展外形参数的估计结果。
图7 半轴长度参数估计结果
可以看到,在滤波初始阶段由于缺乏扩展状态先验信息,扩展外形矩阵滤波初值及其所服从IW 分布的初始参数矩阵选取值与实际值偏差较大,进而导致扩展外形矩阵估计偏差较大,因此基于扩展外形矩阵特征值分解所估计的半轴长度参数值与实际值（短半轴长5 m,长半轴长12 m）存在较大偏差。但随着扩展外形矩阵估计精度及鲁棒性的上升,该方法估计的半轴参数值也随之快速收敛于真值附近,并且偏差较小,因而展现了良好的半轴参数估计性能。至于基于最小二乘（椭球）拟合的半轴长度参数估计方法,由于其直接对带测量误差的雷达等效位置量测开展拟合,因而椭圆体大小受这些量测点空间散布的变化影响较大,导致拟合估计得到的半轴长度参数出现了很大的数值不稳定性。
此外,图8展示了单次运行中两种方法对飞行器主轴方向的估计偏差结果,可以看到本文特征值分解方法所估计的飞行器主轴指向与其真实指向的偏差角大部分处于5°以内,平均值可达到2.22°之低,而最小二乘拟合方法的估计结果不仅振荡区间大,鲁棒性差,平均估计偏差角更是达到24.42°之高,进一步验证了本文特征值分解方法的有效性和优越性。
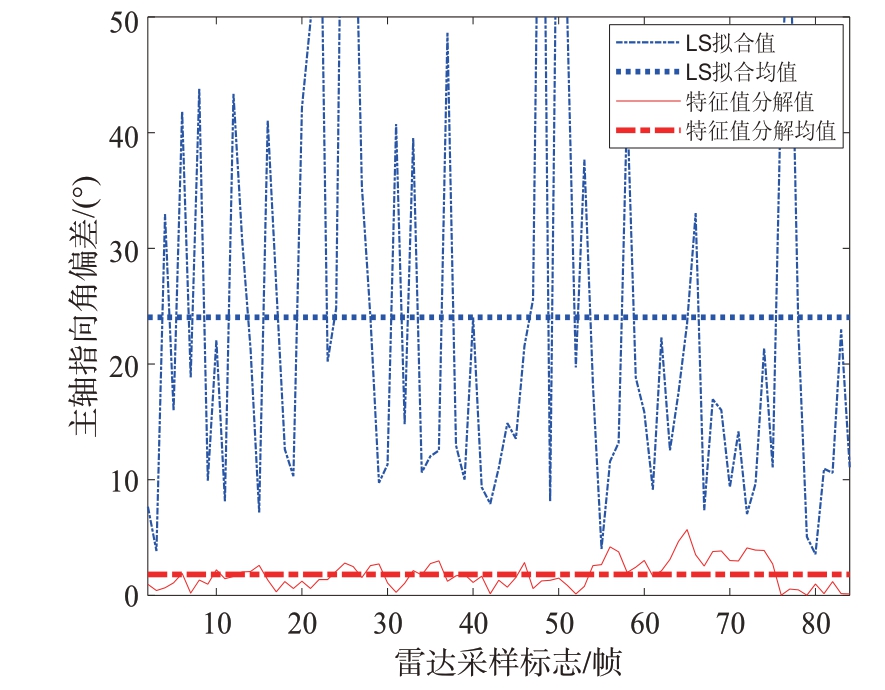
图8 主轴方向估计偏差结果
表3 给出了200 次蒙特卡洛运行及测量精度R2、融合量测数目Num2下,两种方法对飞行器扩展外形参数估计的AEE 结果。可以看到,在同等比较条件下,本文特征值分解方法相比于最小二乘（椭球）拟合方法对各扩展外形参数的估计精度均有大幅提升,其中短半轴长提升84.58%,长半轴长提升97.24%,主轴指向提升91.70%。需说明的是,在量测数据较少（如取Num1）及雷达测量精度变差（如取R3）时,两种方法的估计精度均出现较大恶化（相关作图限于篇幅在此未作展示。其中对于最小二乘拟合方法,限于最小二乘拟合方程求解要求须保证单帧雷达周期内拟合所使用的量测点数不能低于9）,这说明保持融合量测数据的一定冗余性及较高的雷达测量精度是提高扩展目标外形参数估计精度的基本保证。这也是本文采用多部高分辨雷达测量跟踪获取飞行器量测数据的直接原因,同时充分发挥了多传感器测量数据融合估计的优势,为基于运动状态及扩展外形参数的扩展型浮低空飞行器识别分类提供更为有力的信息支撑,并有效提升低空空域态势感知能力。
表3 200次蒙特卡洛运行条件下两种方法的飞行器扩展外形参数AEE估计结果对比
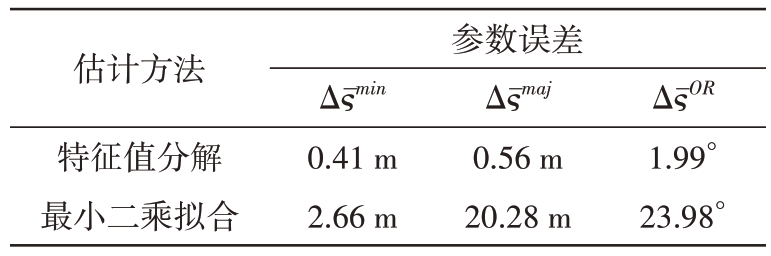
估计方法特征值分解最小二乘拟合参数误差Δςˉmin 0.41 m 2.66 m Δςˉmaj 0.56 m 20.28 m ΔςˉOR 1.99°23.98°
5 结束语
本文在随机矩阵模型和贝叶斯滤波框架下实现了浮低空飞行器运动状态与扩展状态的良好跟踪,使用特征值分解方法得到了飞行器外形参数的较好估计。所得结论为浮低空飞行器的跟踪识别及空域态势感知能力的提升提供有力信息支撑。与此同时,本文尚存在以下几点工作有待进一步思考和研究：
1） 探测相对关系引起的散射中心变化［4,7］。本文假设雷达与飞行器的相对观测几何及相对距离理想,实际场景中这些相对参数的改变会引起飞行器散射中心的强弱、分布及对应的雷达量测数目发生变化,甚至可能引起量测失真问题。
2） 雷达量测转换的强非线性。本文为验证随机矩阵模型应用方便起见,将雷达量测假设为服从高斯分布的等效位置量测,实际上雷达极坐标量测在转换至空间直角坐标系时会发生非线性改变,可能加剧转换量测的非高斯分布特性［20］,这对非线性扩展目标跟踪算法提出了较高的要求。
［1］ 余莎莎,陈星雨.城市空中交通领域关键技术创新与挑战［J］.航空学报,2024,45（S1）:26-47.
［2］ 袁雪,韦楠楠,张兴敢.利用低数据率HRRP 序列进行弹道中段目标识别［J］.雷达科学与技术,2023,21（5）:559-567.
［3］ XU Zhiming, ZHU Yiqi, AI Xiaofeng, et al. Low Scattering Performance and Scattering Center Characteristics of Streamlined Space Target［J］. IEEE Trans on Aerospace and Electronic Systems, 2024,60（2）:1824-1834.
［4］ ZHANG Xiaoxiao, LAN Jian. Measurement Combination Estimator for Multisensor Extended Object Tracking Using Random Matrix［J］. IEEE Trans on Aerospace and Electronic Systems, 2024, 60（1）:698-715.
［5］ KOCH J W. Bayesian Approach to Extended Object and Cluster Tracking Using Random Matrices［J］. IEEE Trans on Aerospace and Electronic Systems, 2008,44（3）:1042-1059.
［6］ FELDMANN M, FRÄNKEN D, KOCH W. Tracking of Extended Objects and Group Targets Using Random Matrices［J］. IEEE Trans on Signal Processing,2011,59（4）:1409-1420.
［7］ LAN Jian. Extended Object Tracking Using Random Matrix with Extension-Dependent Measurement Numbers［J］.IEEE Trans on Aerospace and Electronic Systems,2023,59（4）:4464-4477.
［8］ BAUM M, HANEBECK U D. Random Hypersurface Models for Extended Object Tracking［C］//2009 IEEE International Symposium on Signal Processing and Information Technology, Ajman:IEEE, 2009:178-183.
［9］ TUNCER B, ORGUNER U, ÖZKAN E. Multi-Ellipsoidal Extended Target Tracking with Variational Bayes Inference［J］. IEEE Trans on Signal Processing, 2022,70:3921-3934.
［10］ PEI Shiqi, CHENG Di, CHEN Chang, et al. Multi-Ellipsoidal Tracking of Rotating Extended Object or Target Group［C］//2023 7th International Conference on Information Communication and Signal Processing, Xi’an,China:IEEE, 2023:139-143.
［11］ 程飞龙,金智峰,戚国庆,等.基于随机超曲面模型的机动星凸形扩展目标跟踪［J］.兵器装备工程学报,2024,45（6）:181-187.
［12］ 王旭昕,陈辉,连峰,等.扩展目标多特征估计自适应渐进滤波器［J］.电子学报,2024,52（9）:181-193.
［13］ 任磊,郭云飞.带输入噪声的高斯过程扩展目标跟踪算法［J］.杭州电子科技大学学报（自然科学版）,2022,42（2）:41-48.
［14］ XU Mengdie, YANG Chaoqun, CAO Xiaomeng, et al. Irregular Extended Target Tracking with Unknown Measurement Noise Covariance［J］. Signal Processing,2024,225:1-10.
［15］ 许红,刘欣蕊,邢逸舟,等.基于参数解耦的变分贝叶斯自适应卡尔曼滤波［J］.雷达科学与技术,2024,22（3）:291-299.
［16］ YANG Shishan, BAUM M. Tracking the Orientation and Axes Lengths of an Elliptical Extended Object［J］. IEEE Trans on Signal Processing, 2019,67（18）:4720-4729.
［17］ 马全鑫,杜晓林,董军,等.基于几何方法的结构化协方差矩阵估计［J］.雷达科学与技术,2023,21（2）:143-150.
［18］ 曹震雄,翁顺,李佳靖,等.基于时域残余力向量特征分解的结构损伤方法研究［J］.振动工程学报,2023,36（6）:1516-1526.
［19］ 杜明洋,毕大平,王树亮,等.一种混合的机动目标分离检测跟踪算法［J］.西安交通大学学报,2018,52（10）:116-123.
［20］ 刘政玮,陈映,鲁耀兵.一种高分辨雷达空间目标跟踪方法研究［J］.系统工程与电子技术,2024,46（2）:488-496.